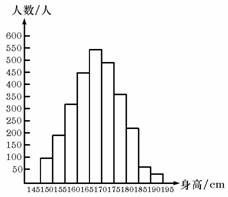
(本题12分)在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)
共有100个数据,将数据分组如右表:
(1)补全频率分布表,并画出频率分布直方图;
(2)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
| 分组 | 频数 | 频率 |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
| 合计 |
|
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
(求平均数时只列出算式即可)
(本题13分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与
吨)与
相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
|
| 3 | 4 | 5 | 6 |
|
| 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式  ,
,![]() )
)
(本小题满分14分)
我市高三年级一模考试后,市教研室为了解情况,随机抽取200名考生的英语成绩统计如下表:
| 英语成绩 | 75~90 | 90~105 | 105~120 | 120~135 | 135~150 |
| 考生人数 | 20 | 30 | 80 | 40 | 30 |
(1)列出频率分布表
(2)画出频率分布直方图及折线图
(3)估计高三年级英语成绩在120分以上的概率
(本小题满分12分)
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂

试分别估计两个分厂生产的零件的优质品率;
由于以上统计数据填下面![]() 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
| 甲 厂 | 乙 厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
附:![]()
 (Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;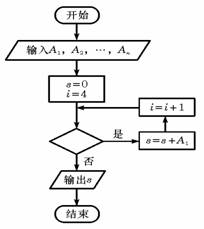 A.i<6 B. i<7 C. i<8 D. i<9
A.i<6 B. i<7 C. i<8 D. i<9