函数y=
-1(x≤0)的反函数是( )
| 3 | x2 |
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
函数f(x)=|sinx+cosx|的最小正周期是( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
表2:
(i)先确定x,y,再在答题纸上完成下列频率分布直方图.就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
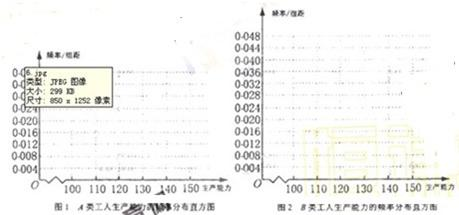
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)
0 27440 27448 27454 27458 27464 27466 27470 27476 27478 27484 27490 27494 27496 27500 27506 27508 27514 27518 27520 27524 27526 27530 27532 27534 27535 27536 27538 27539 27540 27542 27544 27548 27550 27554 27556 27560 27566 27568 27574 27578 27580 27584 27590 27596 27598 27604 27608 27610 27616 27620 27626 27634 266669
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
| 生产能力分组 | [100,110] | [110,120] | [120,130] | [130,140] | [140,150] |
| 人数 | 4 | 8 | x | 5 | 3 |
| 生产能力分组 | [110,120] | [120,130] | [130,140] | [140,150] |
| 人数 | 6 | y | 36 | 18 |

(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)
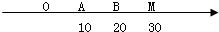 如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y 表示C到A距离4倍与C道B距离的6倍的和.
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y 表示C到A距离4倍与C道B距离的6倍的和.
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.