13.点F(c,0)为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,点P为双曲线左支上一点,线段PF与圆x2+y2=$\frac{{b}^{2}}{4}$相切于点Q,且$\overrightarrow{PQ}$=$\frac{1}{2}$$\overrightarrow{PF}$,则双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
12.某地区汽车限行规定如下:
某地区某行政单位有车牌尾号为6的汽车A和尾号为9的汽车B,在非限行日,A车日出车频率为p,B车日出车频率为q,周六、周日和限行日停止用车,现将汽车日出车频率视为日出车概率,且A,B两车是否出车相互独立.
(1)若p=0.8,求汽车A在同一周内恰有两天连续出车的概率;
(2)若p∈[0.4,0.8],且两车的日出车频率之和为1,为实现节能减排与绿色出行,应如何调控两车的日出车频率,使得一周内汽车A,B同日都出车的平均天数最少.
0 249766 249774 249780 249784 249790 249792 249796 249802 249804 249810 249816 249820 249822 249826 249832 249834 249840 249844 249846 249850 249852 249856 249858 249860 249861 249862 249864 249865 249866 249868 249870 249874 249876 249880 249882 249886 249892 249894 249900 249904 249906 249910 249916 249922 249924 249930 249934 249936 249942 249946 249952 249960 266669
| 车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(1)若p=0.8,求汽车A在同一周内恰有两天连续出车的概率;
(2)若p∈[0.4,0.8],且两车的日出车频率之和为1,为实现节能减排与绿色出行,应如何调控两车的日出车频率,使得一周内汽车A,B同日都出车的平均天数最少.
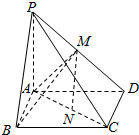 已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.
已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.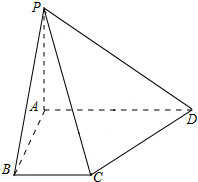 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,且PA=AB=1,CD=$\sqrt{2}$,AD=2.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,且PA=AB=1,CD=$\sqrt{2}$,AD=2.