17.若下表数据对应的y关于x的线性回归方程为$\hat y=0.7x+a$,则a=0.35.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
15.若(2x+$\sqrt{3}$)100=a0+a1x+a2x2+…+a100x100,则(a0+a2+a4+…+a100)2-(a1+a3+a5+…+a99)2的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
14.设6件产品中有4件合格品2件不合格品,从中任意取2件,则其中至少一件是不合格品的概率为( )
| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.7 |
13.在比赛中,如果运动员甲胜运动员乙的概率是$\frac{2}{3}$,那么在五次比赛中,运动员甲恰有三次获胜的概率是( )
| A. | $\frac{40}{243}$ | B. | $\frac{80}{243}$ | C. | $\frac{110}{243}$ | D. | $\frac{20}{243}$ |
12.四名同学报名参加三项课外活动,每人限报其中一项,不同报名方法共有( )
| A. | 12 | B. | 64 | C. | 81 | D. | 7 |
11.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如表所示:
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
附:${Χ^2}=\frac{{n({n_{11}}{n_{22}}-{n_{12}}{n_{21}})2}}{{{n_{11}}{n_{21}}{n_{12}}{n_{22}}}}$
0 247283 247291 247297 247301 247307 247309 247313 247319 247321 247327 247333 247337 247339 247343 247349 247351 247357 247361 247363 247367 247369 247373 247375 247377 247378 247379 247381 247382 247383 247385 247387 247391 247393 247397 247399 247403 247409 247411 247417 247421 247423 247427 247433 247439 247441 247447 247451 247453 247459 247463 247469 247477 266669
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
附:${Χ^2}=\frac{{n({n_{11}}{n_{22}}-{n_{12}}{n_{21}})2}}{{{n_{11}}{n_{21}}{n_{12}}{n_{22}}}}$
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
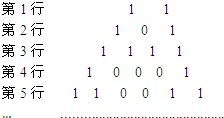 将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表、从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第2n-1行;第62行中1的个数是32.