15．若F1.F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点.A为双曲线的左顶点.以F1.F2为直径的圆交双曲线的——青夏教育精英家教网——

15．若F₁，F₂分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，A为双曲线的左顶点，以F₁，F₂为直径的圆交双曲线的一条渐近线于M，N两点，且满足∠MAN=120°，则双曲线的离心率为（　　）

$\frac{2\sqrt{3}}{3}$

$\frac{\sqrt{21}}{3}$

14．一个几何体的三视图如图所示，则这个几何体的体积为（　　）

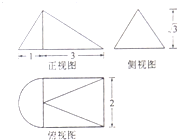
$\frac{（8+π）\sqrt{3}}{6}$

$\frac{（12+π）\sqrt{3}}{6}$

$\frac{（12+π）\sqrt{3}}{2}$

$\frac{（6+π）\sqrt{3}}{3}$

13．已知函数f（x）=sin（2x+φ）（|φ|＜$\frac{π}{2}$），且f（$\frac{π}{12}$）=1，为了得到g（x）=sin2x的图象，则只要将f（x）的图象（　　）

	A．	向左平移$\frac{π}{3}$个单位		B．	向右平移$\frac{π}{3}$个单位
	C．	向左平移$\frac{π}{6}$个单位		D．	向右平移$\frac{π}{6}$个单位

12．若变量x，y满足约束条件$\left\{\begin{array}{l}{2x+3y≥6}\\{x-y≥0}\\{x≤3}\end{array}\right.$，则函数z=2x+y的最大值和最小值分别是（　　）

6和$\frac{18}{5}$

9和$\frac{18}{5}$

11．已知平面向量$\overrightarrow{a}，\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$，$\overrightarrow{b}$=（1，0）且$\overrightarrow{a}$⊥（$\overrightarrow{a}$-2$\overrightarrow{b}$），则|2$\overrightarrow{a}$+$\overrightarrow{b}$|的值为（　　）

10．在等差数列{a_n}中，若2a₃+a₉=33，则数列{a_n}的前9项和等于（　　）

9．设集合A={x|x²-x-2≤0}，B={x|x≥a+1}，若A?B，则a的取值范围是（　　）

8．已知直线l：3x+4y+3=0和圆C：x²+y²-2x-2y+1=0．
（Ⅰ）判断直线l与圆C的位置关系；
（Ⅱ）若P是直线l上的动点，PA是圆C的一条切线，A是切点，求三角形PAC的面积S的最小值．

7．已知m、n是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是（　　）

	A．	若m∥n，m∥α且n∥β，则α∥β??????????
	B．	若m⊥n，m∥α且n∥β，则α⊥β?
	C．	若m∥α且n⊥m，则n⊥α????????????????????
	D．	若m⊥n，m⊥α且n⊥β，则α⊥β

6．设函数f（x）=$\left\{\begin{array}{l}{log_2}x，x＞0\\{4^x}，x≤0\end{array}$则f（f（$\frac{1}{2}$））=$\frac{1}{4}$；若函数g（x）=f（x）-k存在两个零点，则实数k的取值范围是（0.1]．

0 246575 246583 246589 246593 246599 246601 246605 246611 246613 246619 246625 246629 246631 246635 246641 246643 246649 246653 246655 246659 246661 246665 246667 246669 246670 246671 246673 246674 246675 246677 246679 246683 246685 246689 246691 246695 246701 246703 246709 246713 246715 246719 246725 246731 246733 246739 246743 246745 246751 246755 246761 246769 266669