5.用数学归纳法证明“当n为奇数时,xn+yn能被x+y整除”,在验证n=1正确后,归纳假设应写成( )
| A. | 假设n=k(k∈N)时命题成立,即xk+yk能被x+y整除 | |
| B. | 假设n≥k(k∈N)时命题成立,即xk+yk能被x+y整除 | |
| C. | 假设n=2k+1(k∈N*)时命题成立,即x2k+1+y2k+1能被x+y整除 | |
| D. | 假设n=2k-1(k∈N*)时命题成立,即x2k-1+y2k-1能被x+y整除 |
2.已知集合A={x|x2=2},B={1,$\sqrt{2}$,2},则A∩B=( )
| A. | {2} | B. | {$\sqrt{2}$} | C. | {-$\sqrt{2}$,1,$\sqrt{2}$,2} | D. | {1,$\sqrt{2}$,2} |
19.已知x>0,y>0,$\frac{1}{x}+\frac{m}{y}$=1(m>0),若x+y-$\sqrt{{x}^{2}+{y}^{2}}$有最大值,则m的取值范围为( )
0 246461 246469 246475 246479 246485 246487 246491 246497 246499 246505 246511 246515 246517 246521 246527 246529 246535 246539 246541 246545 246547 246551 246553 246555 246556 246557 246559 246560 246561 246563 246565 246569 246571 246575 246577 246581 246587 246589 246595 246599 246601 246605 246611 246617 246619 246625 246629 246631 246637 246641 246647 246655 266669
| A. | ($\frac{1}{2}$,2) | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{4},4$] |
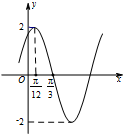 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.