14.某校鲁班学习小组利用课余时间模拟制作奥运圣火采集器,已知他们制作采集器的抛物面的轴切线为经过定点P(1,2)的抛物线,则该抛物线的焦点与双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1在一三象限内的渐近线的距离为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$或$\frac{1}{16}$ | C. | $\frac{1}{16}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
10.如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )?


| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
9.已知函数f(x)=x2-4x+3,集合M={(x,y)|f(x)+f(y)≤0},集合N={(x,y)|f(x)-f(y)≥0},则集合M∩N面积为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3π}{2}$ |
7.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的零点A,B,若|AF|=3|FB|,则k的值是( )
0 246407 246415 246421 246425 246431 246433 246437 246443 246445 246451 246457 246461 246463 246467 246473 246475 246481 246485 246487 246491 246493 246497 246499 246501 246502 246503 246505 246506 246507 246509 246511 246515 246517 246521 246523 246527 246533 246535 246541 246545 246547 246551 246557 246563 246565 246571 246575 246577 246583 246587 246593 246601 266669
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
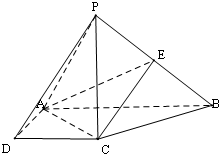 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.
 如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.