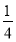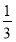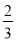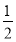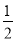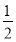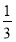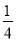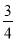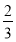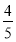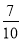随机询问100名性别不同的大学生是否爱好踢毽子运动,得到如下的列联表:
| 男 | 女 | 总计 |
爱好 | 10 | 40 | 50 |
不爱好 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
附表:
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算,统计量K2=4.762,参照附表,得到的正确结论是( ).
A.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C.有97.5%以上的把握认为“爱好该项运动与性别有关”
D.有97.5%以上的把握认为“爱好该项运动与性别无关”
在2013年3月15日这天,郑州市物价部门对本市5家商场某商品一天的销售量及其价格进行了调查,5家商场某商品的销售价格x(元)与销售量y(件)之间的一组数据如下表:
价格x | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y | 11 | 10 | 8 | 6 | 5 |
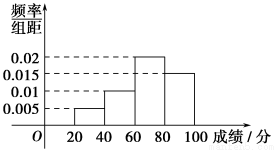
作出散点图,可知销售量y与价格x之间具有线性相关关系,其线性回归方程是 =-3.2x+
=-3.2x+ 则实数
则实数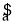 的值是________.
的值是________.
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 |
男生 |
| 6 |
|
女生 | 10 |
|
|
合计 |
|
| 48 |
已知在全班48人中随机抽取1人,抽到喜爱打篮球的学生的概率为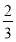 .
.
(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与数学期望.
下面的临界值表供参考:
P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式)χ2=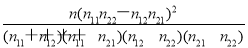 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=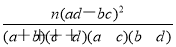 ,其中n=a+b+c+d)
,其中n=a+b+c+d)