(本小题满分12分)
某校举办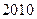 年上海世博会知识竞赛,从参赛的高一、高二学生中各抽
年上海世博会知识竞赛,从参赛的高一、高二学生中各抽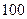 人的成绩作
人的成绩作
 |  | 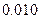 | 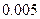 |  |
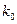 | 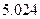 | 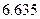 | 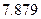 | 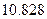 |
参考数据:
| | 高一 | 高二 | 合计 |
| 合格人数 |  | 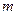 | 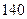 |
| 不合格人数 | 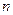 | 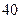 |  |
| 合计 | 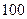 | 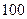 | 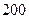 |
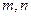 的值;
的值;(Ⅱ)你有多大的把握认为“高一、高二两个年级这次世博会知识竞赛的成绩有差异”.
(本小题满分14分)
为了检测某种产品的直径(单位mm),抽取了一个容量为100的样本,其频率分布表(不完整)如下:
| 分组 | 频数累计 | 频数 | 频率 |
| [10.75,10.85) | 6 | 6 | 0.06 |
| [10.85,10.95) | 15 | 9 | 0.09 |
| [10.95,11.05) | 30 | 15 | 0.15 |
| [11.05,11.15) | 48 | 18 | 0.18 |
| [11.15,11.25) | ▲ | ▲ | ▲ |
| [11.25,11.35) | 84 | 12 | 0.12 |
| [11.35,11.45) | 92 | 8 | 0.08 |
| [11.45,11.55) | 98 | 6 | 0.06 |
| [11.55,11.65) | 100 | 2 | 0.02 |
(Ⅰ)完成频率分布表;
(Ⅱ)画出频率分布直方图;
(Ⅲ)据上述图表,估计产品直径落在
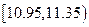 范围内的可能性是百分之几?
范围内的可能性是百分之几?
(本题满分12分)某农科所对冬季昼夜温差与某反季节大豆种子发芽多少之间的关系进行分析研究,他们记录了12月1日至5日的昼夜温差与每天100颗种子的发芽数,数据如下表:
| 日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差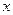 (0C) (0C) | 10 | 11 | 13 | 12 | 8 |
发芽数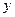 (颗) (颗) | 23 | 25 | 30 | 26 | 16 |
(1) 若先选取的是12月1日和5日的数据,请根据2日至4日的三组数据,求
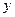 关于
关于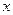 的线性回归方程
的线性回归方程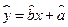 ;
; (2) 若由回归方程得到的估计数据与检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试判断(1)中所得的线性回归方程是否可靠?说明理由.
(本小题满分12分)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下表所示:
零件的个数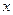 (个) (个) | 2 | 3 | 4 | 5 |
加工的时间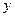 (小时) (小时) | 2.5 | 3 | 4 | 4.5 |
(Ⅱ)求出
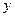 关于
关于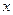 的线性回归方程
的线性回归方程 ,
,并在坐标系中画出回归直线;
(Ⅲ)试预测加工10个零件需要多少时间?
 户居民去年的月均用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下,其中直方图从左到右前
户居民去年的月均用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下,其中直方图从左到右前 个小矩形的面积之比为
个小矩形的面积之比为 ,试估计:
,试估计: ~
~ 内
内 )
)
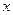 (千万元)
(千万元) (百万元)
(百万元) 相关关系;
相关关系;
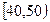 ,
,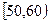 …
…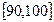 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: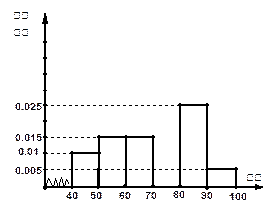
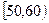 ,
,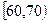 …
… 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
 ,
, …
… 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题