某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2) 试预测加工10个零件需要多少时间?
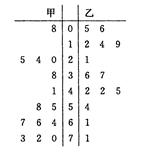
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图判断哪位选手的成绩较稳定?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
下表是关于某设备的使用年限(年)和所需要的维修费用y (万元)的几组统计数据:
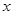 | 2 | 3 | 4 | 5 | 6 |
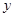 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
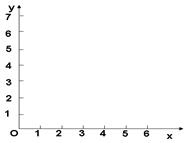
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程
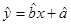 ;
;(3)估计使用年限为10年时,维修费用为多少?
(参考数值:
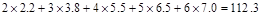 )
)参考公式:
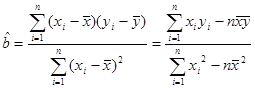 ;
;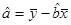 ;
; 甲、乙两人在相同条件下各射击10次,每次命中的环数如下:
| 甲 | 8 | 6 | 7 | 8 | 6 | 5 | 9 | 10 | 4 | 7 |
| 乙 | 6 | 7 | 7 | 8 | 6 | 7 | 8 | 7 | 9 | 5 |
(1)分别计算以上两组数据的平均数;
(2)分别计算以上两组数据的方差;
公式:

(3)根据计算结果,估计一下两人的射击情况.
(本小题满分12分)
以下是测得的某种产品的广告费支出x与销售额y(单位:百万元)之间,有如下的对应数据:
| 广告费支出x | 2 | 4 | 5 | 6 | 8 |
| 销售额y | 30 | 40 | 60 | 50 | 70 |
(2)求y关于x的回归直线方程;
(3)预测当广告费支出为2(百万元)时,则这种产品的销售额为多少(百万元)
某种产品的广告费支出x与销售额y(单位:百万元)之间的一般规律:
(本小题满分12分)一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)表中a= ,b = ;
(Ⅱ)画出频率分布直方图;
(Ⅲ)用频率分布直方图,求出总体的众数及平均数的估计值.
频率分布表
| 分组 | 频数 | 频率 | 频率/组距 |
| (10,20] | 2 | 0.10 | 0.010 |
| (20,30] | 3 | 0.15 | 0.015 |
| (30,40] | 4 | 0.20 | 0.020 |
| (40,50] | a | b | 0.025 |
| (50,60] | 4 | 0.20 | 0.020 |
| (60, 70] | 2 | 0.10 | 0.010 |
频率分布直方图
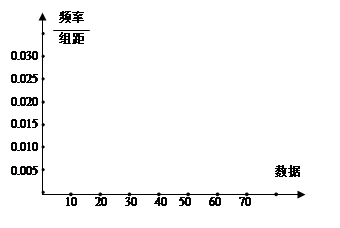


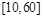 间的频率是多少?
间的频率是多少?