某同学在研究性学习中,收集到某制药厂车间工人数(单位:十人)与药品产量(单位:万盒)的数据如表所示:
| 工人数:x(单位:十人) | 1 | 2 | 3 | 4 |
| 药品产量:y(单位:万盒) | 3 | 4 | 5 | 6 |
(1)请画出如表数据的散点图;
(2)参考公式,根据表格提供的数据,用最小二乘法求出y关于x的线性回归方程y=
 x+
x+ ;(参考数据
;(参考数据 i2=30,
i2=30,
 =50)
=50)(3)试根据(2)求出的线性回归方程,预测该制药厂车间工人数为45时,药品产量是多少?
打鼾不仅影响别人休息,而且可能与患某种疾病有关.下表是一次调查所得的数据,(1)将本题的2*2联表格补充完整。
(2)用提示的公式计算,每一晚都打鼾与患心脏病有关吗?
提示:
| | 患心脏病 | 未患心脏病 | 合计 |
| 每一晚都打鼾 | 3 | 17 | a = |
| 不打鼾 | 2 | 128 | b = |
| 合计 | c = | d = | n = |
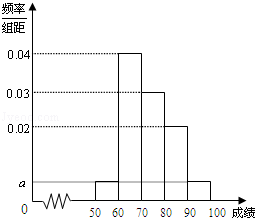
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
某汽车厂生产的A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| | 轿车A | 轿车B | 轿车C |
| 舒适性 | 800 | 450 | 200 |
| 标准型 | 100 | 150 | 300 |
(Ⅰ)在这个月生产的轿车中,用分层抽样的方法抽取n辆,其中有A类轿车45辆,求n的值;
(Ⅱ)在C类轿车中,用分层抽样的方法抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从A类舒适型轿车中抽取10辆,经检测它们的得分如下:,8.7,9.3,8.2,9.4,8.6,9.2,9.6,9.0,8.4,8.6,把这10辆轿车的得分看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过0.6的概率.
某校学习小组开展“学生数学成绩与化学成绩的关系”的课题研究,对该校高二年级800名学生上学期期 数学和化学成绩,按优秀和不优秀分类得结果:数学和化学都优秀的有60人,数学成绩优秀但化学不优秀的有140人,化学成绩优秀但数学不优秀的有100人.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
| | 数学优秀 | 数学不优秀 | 总计 |
| 化学优秀 | | | |
| 化学不优秀 | | | |
| 总计 | | | |
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | 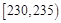 | 8 | 0.16 |
| 第二组 | 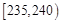 | ① | 0.24 |
| 第三组 | 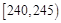 | 15 | ② |
| 第四组 | 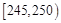 | 10 | 0.20 |
| 第五组 | 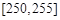 | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
 名学生的成绩得到频率分布直方图如下图所示:
名学生的成绩得到频率分布直方图如下图所示: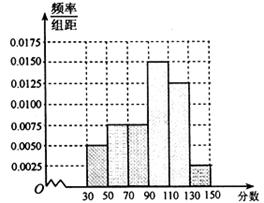
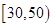 和
和 的学生中共抽取
的学生中共抽取 人,该
人,该 人,求分数在
人,求分数在 人的概率.
人的概率.  的估计值.
的估计值.