已知x与y之间的几组数据如下表:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
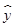 =
= x+
x+ ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).A.
 >b′,
>b′, >a′ B.
>a′ B. >b′,
>b′, <a′
<a′C.
 <b′,
<b′, >a′ D.
>a′ D. <b′,
<b′, <a′
<a′ 通过随机询问110名性别不同的人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
| | 男 | 女 | 总计 |
| 走天桥 | 40 | 20 | 60 |
| 走斑马线 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
 ,得K2=
,得K2= ≈7.8.
≈7.8.附表:
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
A.有99%以上的把握认为“选择过马路的方式与性别有关”
B.有99%以上的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
对一批产品的长度(单位:mm)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为 ( ).
| A.0.09 | B.0.20 | C.0.25 | D.0.45 |
以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分)
已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( ).
| A.2,5 | B.5,5 | C.5,8 | D.8,8 |
某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n等( ).
| A.9 | B.10 | C.12 | D.13 |
随机询问100名性别不同的大学生是否爱好踢毽子运动,得到如下的列联表:
| | 男 | 女 | 总计 |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
A.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C.有97.5%以上的把握认为“爱好该项运动与性别有关”
D.有97.5%以上的把握认为“爱好该项运动与性别无关”
某实验中学共有职工150人,其中高级职称的职工15人,中级职称的职工45人,一般职员90人,现采用分层抽样抽取容量为30的样本,则抽取的高级职称、中级职称、一般职员的人数分别为( )
| A.5、10、15 | B.3、9、18 |
| C.3、10、17 | D.5、9、16 |
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
 算得,K2=
算得,K2= ≈7.8.
≈7.8.附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
A.有99%以上的把握认为“爱好该项运动与性别有关”
B.有99%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且 =2.347x-6.423;
=2.347x-6.423;
②y与x负相关且 =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且 =5.437x+8.493;
=5.437x+8.493;
④y与x正相关且 =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
| A.①② | B.②③ |
| C.③④ | D.①④ |
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
| A.588 | B.480 |
| C.450 | D.120 |