设m,n是两条不同的直线,α,β,γ是三个不同的平面,有以下四个命题:
①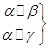 ⇒β∥γ②
⇒β∥γ②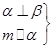 ⇒m⊥β③
⇒m⊥β③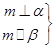 ⇒α⊥β④
⇒α⊥β④ ⇒m∥α
⇒m∥α
其中正确的命题是( )
| A.①④ | B.②③ | C.①③ | D.②④ |
设直线m与平面α相交但不垂直,则下列说法中正确的是( )
| A.在平面α内有且只有一条直线与直线m垂直 |
| B.过直线m有且只有一个平面与平面α垂直 |
| C.与直线m垂直的直线不可能与平面α平行 |
| D.与直线m平行的平面不可能与平面α垂直 |
如图,PA⊥正方形ABCD,下列结论中不正确的是( )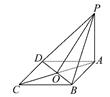
| A.PB⊥CB | B.PD⊥CD |
| C.PD⊥BD | D.PA⊥BD |
已知两条直线m,n,两个平面α,β,给出下面四个命题:
①m∥n,m⊥α⇒n⊥α;
②α∥β,m?α,n?β⇒m∥n;
③m∥n,m∥α⇒n∥α;
④α∥β,m∥n,m⊥α⇒n⊥β.
其中正确命题的序号是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
若α,β是两个相交平面,点A不在α内,也不在β内,则过点A且与α和β都平行的直线( )
| A.只有1条 | B.只有2条 |
| C.只有4条 | D.有无数条 |
设α,β是两个不同的平面,m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分不必要条件是( )
| A.m∥β且l1∥α | B.m∥β且n∥l2 |
| C.m∥β且n∥β | D.m∥l1且n∥l2 |
a,b,c为三条不重合的直线,α,β,γ为三个不重合平面,现给出六个命题:
① ⇒a∥b ②
⇒a∥b ② ⇒a∥b
⇒a∥b
③ ⇒α∥β ④
⇒α∥β ④ ⇒α∥β
⇒α∥β
⑤ ⇒α∥a ⑥
⇒α∥a ⑥ ⇒a∥α
⇒a∥α
其中正确的命题是( )
| A.①②③ | B.①④⑤ |
| C.①④ | D.①③④ |
下列命题中正确的个数是( )
①若直线a不在α内,则a∥α;
②若直线l上有无数个点不在平面α内,则l∥α;
③若l与平面α平行,则l与α内任何一条直线都没有公共点;
④平行于同一平面的两直线可以相交.
| A.1 | B.2 | C.3 | D.4 |
下面四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是( )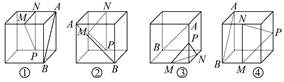
| A.①② | B.①④ | C.②③ | D.③④ |
已知直线m,n和平面α,则m∥n的一个必要不充分条件是( )
| A.m∥α,n∥α | B.m⊥α,n⊥α |
| C.m∥α,n?α | D.m,n与α成等角 |