如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为
 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如 ,
, ,
, , ,则第10行第4个数(从左往右数)为( )
, ,则第10行第4个数(从左往右数)为( )
A. | B. |
C. | D. |
数列{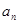 }的通项公式是
}的通项公式是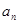 =
= (
( ),那么
),那么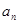 与
与 的大小关系是( )
的大小关系是( )
A.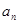 > > | B.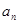 < < |
C.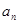 = =  | D.不能确定 |
已知函数 的图象在点
的图象在点 处的切线的斜率为3,数列
处的切线的斜率为3,数列
的前 项和为
项和为 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知数列 为等差数列,
为等差数列,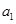 +
+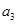 +
+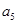
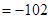 ,
,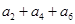
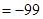 ,以
,以 表示
表示 的前
的前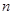 项和,则使得
项和,则使得 达到最小值的
达到最小值的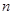 是( )
是( )
| A.37和38 | B.38 | C.37 | D.36和37 |
已知数列 满足
满足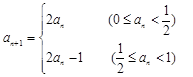 若
若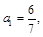 则
则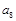 的值为( )
的值为( )
A.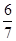 | B.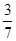 | C.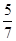 | D.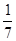 |
下面是关于公差 的等差数列
的等差数列 的四个命题
的四个命题



其中的真命题为
A. | B. | C. | D. |
数列{an}的通项公式 (
( ),若前n项的和
),若前n项的和 ,则项数n为
,则项数n为
A.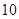 | B.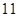 | C.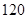 | D. |
已知等比数列 中,公比
中,公比 若
若 则
则 有( )
有( )
| A.最小值-4 | B.最大值-4 | C.最小值12 | D.最大值12 |
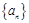 的各项均为正数,且
的各项均为正数,且 ,则
,则








 的图象在点
的图象在点 处的切线的斜率为3,数列
处的切线的斜率为3,数列 的前
的前 项和为
项和为 ,则
,则 的值为( )
的值为( )


