定义平面向量之间的一种运算“⊙”如下：对任意向量ab令
a⊙b，则下列说法错误的是（    ）

A．对任意的a⊙ba⊙(b)

B．a⊙bb⊙a

C．a⊙babab

D．若a与b共线，则a⊙b

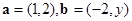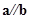设向量，若，则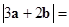

A．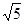

B．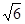

C．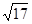

D．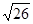

已知向量，若则

A．

B．

C．1

D．3

已知点，O为坐标原点，点P（x，y）的坐标x，y满足   
则向量方向上的投影的取值范围是

A．	B．[-3，3]
C．	D．

已知均为单位向量，它们的夹角为60°，那么等于：

A．

B．

C．

D．4

若，则为（   ）

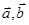平面向量，已知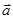＝（4，3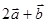），＝（3，18），则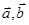夹角的余弦值等于 

A．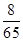

B．－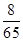

C．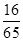

D．－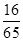

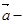已知=（3，1）， =（，5）则32= (    )

A．（2，7）

B．（13，）

C．（2，）

D．（13，13）

若向量，，若，则向量与的夹角为（   ）

A．

B．

C．

D．

设是单位向量，且，则（-）的最小值为（ ）

A．

B．

C．

D．