给定命题p:函数y=sin 和函数y=cos
和函数y=cos 的图象关于原点对称;命题q:当x=kπ+
的图象关于原点对称;命题q:当x=kπ+ (k∈Z)时,函数y=
(k∈Z)时,函数y= (sin 2x+cos 2x)取得极小值.下列说法正确的是( )
(sin 2x+cos 2x)取得极小值.下列说法正确的是( )
| A.p∨q是假命题 | B.¬p∧q是假命题 |
| C.p∧q是真命题 | D.¬p∨q是真命题 |
已知函数y=Asin(ωx+φ)+k(A>0,ω>0)的最大值为4,最小值为0,最小正周期为 ,直线x=
,直线x= 是其图象的一条对称轴,则下面各式中符合条件的解析式为 ( )
是其图象的一条对称轴,则下面各式中符合条件的解析式为 ( )
A.y=4sin | B.y=2sin +2 +2 |
C.y=2sin +2 +2 | D.y=2sin +2 +2 |
设函数f(x)=sin  +sin
+sin  (ω>0)的最小正周期为π,则( )
(ω>0)的最小正周期为π,则( )
A.f(x)在 上单调递减 上单调递减 | B.f(x)在 上单调递增 上单调递增 |
C.f(x)在 上单调递增 上单调递增 | D.f(x)在 上单调递减 上单调递减 |
若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω=( )
| A.5 | B.4 | C.3 | D.2 |
已知sin α-cos α= ,α∈(0,π),则tan α=( )
,α∈(0,π),则tan α=( )
| A.-1 | B.- | C. | D.1 |
已知函数y=Asin(ωx+φ)+m的最大值为4,最小值为0.两个对称轴间最短距离为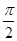 ,直线x=
,直线x= 是其图象的一条对称轴,则符合条件的解析式为( )
是其图象的一条对称轴,则符合条件的解析式为( )
A.y=4sin  | B.y=-2sin  +2 +2 |
C.y=-2sin  | D.y=2sin  +2 +2 |
已知a∈R,sin α+2cos α=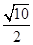 ,则tan 2α=( )
,则tan 2α=( )
A.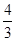 | B. | C.- | D.-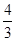 |
 的值是( )
的值是( ) ,则函数g(x)=asinx+cosx的最大值是( )
,则函数g(x)=asinx+cosx的最大值是( )



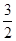 )时,f(x)=sinπx,f
)时,f(x)=sinπx,f =0,则函数f(x)在区间[0,6]上的零点个数是( )
=0,则函数f(x)在区间[0,6]上的零点个数是( )