已知 为定义在
为定义在 上的可导函数,且
上的可导函数,且 对于
对于 恒成立,设
恒成立,设 (
( 为自然对数的底), 则
为自然对数的底), 则
A. | B. |
C. | D. 与 与 的大小不确定 的大小不确定 |
已知曲线 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为 。
,则切点的横坐标为 。
| A.3 | B.2 | C.1 | D. |
设 是定义在R上的奇函数,且f(2)=0,当x>0时,有
是定义在R上的奇函数,且f(2)=0,当x>0时,有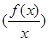 的导数<0恒成立,则不等式
的导数<0恒成立,则不等式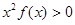 的解集是:
的解集是:
A.(一2,0)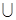 (2,+ (2,+  ) ) | B.(一2,0)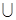 (0,2) (0,2) |
C.(-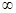 ,-2) ,-2)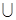 (2,+ (2,+ 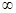 ) ) | D.(-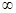 ,-2) ,-2)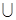 (0,2) (0,2) |
如图,函数y= 的图象在点P处的切线方程是y=-x+8,则f(5)+f’(5)=
的图象在点P处的切线方程是y=-x+8,则f(5)+f’(5)=
A. | B.1 | C.2 | D.0 |
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,g(-2)=0且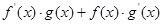 >0,则 不等式g (x)
>0,则 不等式g (x) f(x) <0的解集是( )
f(x) <0的解集是( )
| A.(-2, 0)∪(2,+ ∞) | B.(-2, 0)∪(0,2) |
| C.(-∞, -2)∪(2,+ ∞) | D.(-∞, -2)∪(0,2) |
已知函数f(x)的导函数为 ,且满足f(x)=2x
,且满足f(x)=2x +ln x,则
+ln x,则 = ( )
= ( )
| A.-e | B.-1 | C.1 | D.e |
若函数 的导函数是
的导函数是 ,则函数
,则函数

的单调递减区间是
A. | B. , , |
C. | D. , , |
等比数列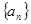 中,
中,  ,函数
,函数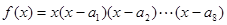 ,则
,则
A.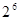 | B.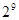 | C.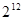 | D.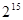 |
曲线 在点
在点 处的切线与直线
处的切线与直线 和
和 围成的三角形的面积为
围成的三角形的面积为
A. | B. | C. | D.1 |
 在点
在点 处的切线与直线
处的切线与直线 平行,若数列
平行,若数列 的前n项和为
的前n项和为 ,则
,则 的值为( )
的值为( )


