设函数f(x)=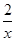 +ln x,则( ).
+ln x,则( ).
A.x=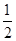 为f(x)的极大值点 为f(x)的极大值点 |
B.x=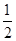 为f(x)的极小值点 为f(x)的极小值点 |
| C.x=2为f(x)的极大值点 |
| D.x=2为f(x)的极小值点 |
直线y=kx+b与曲线y=x3+ax+1相切于点(2,3),则b的值为( ).
| A.-3 | B.9 | C.-15 | D.-7 |
已知函数y=f(x),其导函数y=f′(x)的图象如图所示,则y=f(x) ( ).
| A.在(-∞,0)上为减函数 |
| B.在x=0处取极小值 |
| C.在(4,+∞)上为减函数 |
| D.在x=2处取极大值 |
由曲线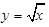 ,直线
,直线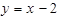 及
及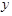 轴所围成的封闭图形的面积为( )
轴所围成的封闭图形的面积为( )
A.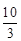 | B.4 | C.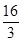 | D.6 |
已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则( ).
| A.当k=1时,f(x)在x=1处取到极小值 |
| B.当k=1时,f(x)在x=1处取到极大值 |
| C.当k=2时,f(x)在x=1处取到极小值 |
| D.当k=2时,f(x)在x=1处取到极大值 |
设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( ).
| A.?x∈R,f(x)≤f(x0) |
| B.-x0是f(-x)的极小值点 |
| C.-x0是-f(x)的极小值点 |
| D.-x0是-f(-x)的极小值点 |
由直线x=-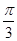 ,x=
,x=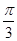 ,y=0与曲线y=cos x围成的封闭图形的面积为( ).
,y=0与曲线y=cos x围成的封闭图形的面积为( ).
A. | B.1 | C.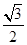 | D. |
已知函数f(x)的导函数f′(x),且满足f(x)=2xf′(1)+ln x,则f′(1)=( ).
| A.-e | B.-1 | C.1 | D.e |
函数y=xex在点(1,e)处的切线方程为( ).
| A.y=ex | B.y=x-1+e |
| C.y=-2ex+3e | D.y=2ex-e |