曲线y=ex在点A(0,1)处的切线的斜率为 ( ).
| A.1 | B.2 |
| C.e | D. |
曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵坐标为 ( ).
| A.-9 | B.-3 |
| C.9 | D.15 |
下列结论:①(cos x)′=sin x;② ′=cos
′=cos ;③若y=
;③若y= ,则y′|x=3
,则y′|x=3
=- ;④(e3)′=e3.其中正确的个数为 ( ).
;④(e3)′=e3.其中正确的个数为 ( ).
| A.0个 | B.1个 |
| C.2个 | D.3个 |
曲线y=x3在点P处的切线的斜率为3,则P点的坐标为 ( ).
| A.(-2,-8) | B.(-1,-1),(1,1) |
| C.(2,8) | D.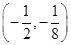 |
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正确结论的序号是( )
| A.①③ | B.①④ |
| C.②③ | D.②④ |
设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( )
| A.?x∈R,f(x)≤f(x0) |
| B.-x0是f(-x)的极小值点 |
| C.-x0是-f(x)的极小值点 |
| D.-x0是-f(-x)的极小值点 |
函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为( )
| A.{x|x>0} | B.{x|x<0} |
| C.{x|x<-1或x>1} | D.{x|x<-1或0<x<1} |
直线y=a与函数y=x3-3x的图象有三个相异的交点,则a的取值范围为 ( ).
| A.(-2,2) | B.[-2,2] |
| C.[2,+∞) | D.(-∞,-2] |
函数y=1+3x-x3有 ( ).
| A.极小值-1,极大值1 | B.极小值-2,极大值3 |
| C.极小值-2,极大值2 | D.极小值-1,极大值3 |
函数f(x)=x+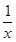 在x>0时有 ( ).
在x>0时有 ( ).
| A.极小值 | B.极大值 |
| C.既有极大值又有极小值 | D.极值不存在 |