若函数y=loga|x-2|(a>0且a≠1)在区间(1,2)上是增函数,则f(x)在区间(2,
+∞)上的单调性为 ( )
| A.先增后减 | B.先减后增 |
| C.单调递增 | D.单调递减 |
设函数 ,若
,若 ,则实数
,则实数 ( )
( )
A. 1或3 1或3 | B. 1 或0 1 或0 | C.3或0 | D. 1或0或3 1或0或3 |
已知数列 满足
满足 ,若正整数
,若正整数 满足
满足 为整数,则称
为整数,则称 叫做企盼数,那么区间
叫做企盼数,那么区间 内所有的企盼数的和为( )
内所有的企盼数的和为( )
| A.1001 | B.2044 | C.2030 | D.2026 |
若logm9<logn9<0,那么m,n满足的条件是( )
| A.m>n>1 | B.0<n<m<1 | C.n>m>1 | D.0<m<n<1 |
函数y=log (2x2-3x+1)的递减区间为 ( )
(2x2-3x+1)的递减区间为 ( )
A.(1,+ ) ) | B.(-  , , ] ] | C.( ,+ ,+ ) ) | D.(- , , ] ] |
已知函数
 ,则
,则 的值是 ( )
的值是 ( )
| A.9 | B. | C.-9 | D.- |
已知函数f(x)=3-2|x|,g(x)=x2-2x,构造函数F(x),定义如下:当f(x)≥g(x)
时,F(x)=g(x);当f(x)<g(x)时,F(x)=f(x).那么F(x) ( )
A.有最大值7-2 ,无最小值 ,无最小值 | B.有最大值3,最小值-1 |
| C.有最大值3,无最小值 | D.无最大值,也无最小值 |
设函数
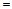
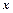 |
|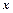 | + b
| + b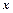 + c 给出下列四个命题:
+ c 给出下列四个命题:
①c = 0时,y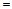
 是奇函数 ②b
是奇函数 ②b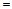 0 , c >0时,方程
0 , c >0时,方程
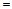 0 只有一个实根
0 只有一个实根
③y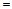
 的图象关于(0 , c)对称 ④方程
的图象关于(0 , c)对称 ④方程
 0至多两个实根
0至多两个实根
其中正确的命题是 ( )
| A.①、④ | B.①、③ | C.①、②、③ | D.①、②、④ |
当 时,函数
时,函数 在
在 时取得最大值,则a的取值范围是
时取得最大值,则a的取值范围是
A. | B. | C. | D. |
设f(x)= 则f(ln3)= ( )
则f(ln3)= ( )
A. | B.ln3-1 | C.e | D.3e |