函数f(x)=ax2+bx+c(a≠0)的图象关于直线 对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )
对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )
| A.{1,3} | B.{2,4} | C.{1,2,3,4} | D.{1,2,4,8} |
已知函数 的定义域为
的定义域为 ,若存在常数
,若存在常数 ,对任意
,对任意 ,有
,有 ,则称
,则称 为
为 函数.给出下列函数:
函数.给出下列函数:
① ; ②
; ② ; ③
; ③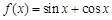 ; ④
; ④ ;
;
⑤ 是定义在R上的奇函数,且满足对一切实数
是定义在R上的奇函数,且满足对一切实数 均有
均有 .其中是
.其中是 函数的序号是( )
函数的序号是( )
| A.①②④ | B.①②⑤ | C.①③④ | D.①④⑤ |
已知函数 (
( 且
且 )满足
)满足 ,则
,则 的解为( )
的解为( )
A. | B. | C. | D. |
若函数 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
 若
若 是
是 的最小值,则
的最小值,则 的取值范围为( ).
的取值范围为( ).
| A.[-1,2] | B.[-1,0] | C.[1,2] | D. |
若 的最小值是
的最小值是
A. | B. | C. | D. |
 、
、 满足
满足 ,则称
,则称 上的一组正交函数,给出三组函数:①
上的一组正交函数,给出三组函数:① ;②
;② ;③
;③ .
. ,若
,若 ,则
,则 ( )
( )



 ,高为1m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是 ( )
,高为1m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是 ( )
 则下列结论正确的是( )
则下列结论正确的是( ) 是偶函数 B.
是偶函数 B. 