设函数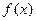 和g(x
和g(x )分别是R上的偶函数和奇函数,则下列结论恒成立的是
)分别是R上的偶函数和奇函数,则下列结论恒成立的是
A.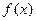 +|g(x)|是偶函数 +|g(x)|是偶函数 | B.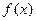 -|g(x)|是奇函数 -|g(x)|是奇函数 |
C.|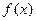 | +g(x)是偶函数 | +g(x)是偶函数 | D.|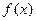 |- g(x)是奇函数 |- g(x)是奇函数 |
函数y=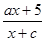 的反函数的图象关于点(–2,3)对称,则f(x)的单调性为 ( )
的反函数的图象关于点(–2,3)对称,则f(x)的单调性为 ( )
| A.在(-∞,-2)和(-2,+∞)上递增 | B.在(-∞,-3)和(-3,+∞)上递增 |
| C.在(-∞,-3)和(-3,+∞)上递减 | D.与a、c的值有关,不能确定 |
设函数 ,则它的图象关于 ( )
,则它的图象关于 ( )
| A.x轴对称 | B.y轴对称 | C.原点对称 | D.直线 对称 对称 |
设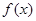 是周期为2的奇函数,当0≤x≤1时,
是周期为2的奇函数,当0≤x≤1时,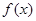 =
=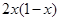 ,则
,则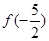 =( )
=( )
A.-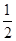 | B.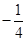 | C.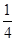 | D.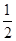 |
下列函数中,既是 偶函数,又在区间
偶函数,又在区间 上单调递减的函数是( )
上单调递减的函数是( )
A. | B. | C. | D. |
函数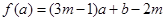 ,当
,当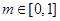 时,
时,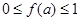 恒成立,则
恒成立,则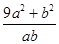
的最大值与最小值之和为 ( )
| A. 18 | B. 16 | C. 14 | D.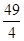 |
设 ,则此函数在区间(0,1)内为( )
,则此函数在区间(0,1)内为( )
| A.单调递减, | B.有增有减 | C.单调递增, | D.不确定 |
函数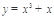 的递增区间是( )
的递增区间是( )
A.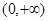 | B.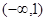 | C.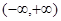 | D.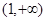 |
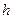 随时间
随时间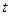 变化的图象可能是( )
变化的图象可能是( )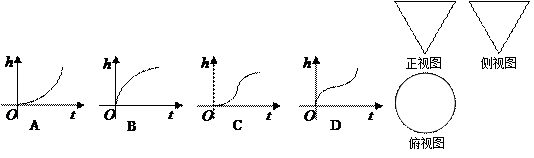

 ,则函数
,则函数 的图像大致是
的图像大致是 