若f(x)是R上周期为5的奇函数,且满 足f(1)=1,f(2)=2,则f(8)-f(4)= ( )
| A.-1 | B.1 | C.-2 | D.2 |
函数y= 的值域是( )
的值域是( )
| A.[0,+∞) | B.[0,3] | C.[0,3) | D.(0,3) |
若函数 的定义域是
的定义域是 ,则函数
,则函数 的定义域( )
的定义域( )
A. | B. | C. | D. |
函数y=1- ( )
( )
| A.在(-1,+∞)上单调递增 | B.在(-1,+∞)上单调递减 |
| C.在(1,+∞)上单调递增 | D.在(1,+∞)上单调递减 |
已知函数 ,则下列判断中正确的是( )
,则下列判断中正确的是( )
| A.奇函数,在R上为增函数 | B.偶函数,在R上为增函数 |
| C.奇函数,在R上为减函数 | D.偶函数,在R上为减函数 |
函数 的定义域为( )
的定义域为( )
A.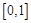 | B.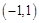 | C. | D.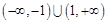 |
已知函数 的定义域为R,则m的取值范围是( )
的定义域为R,则m的取值范围是( )
A. | B. | C. | D. |
若函数 (
( 为常数)是奇函数,则
为常数)是奇函数,则 的值是( )
的值是( )
A. | B.0 | C.1 | D.2 |

 ( )
( )