若函数f(x)是定义在R上的偶函数,且对任意x∈R,总有f(x+2)=-f(x)成立,则f(19)等于( )
| A.0 | B.1 | C.18 | D.19 |
方程1-x-xlnx=0的根的个数为( )个
| A.3 | B.2 | C.1 | D.0 |
设函数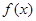 的零点为
的零点为 ,函数
,函数 的零点为
的零点为 ,若
,若
,则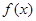 可以是( )
可以是( )
A. | B. |
C. | D.㏑(8x-2) |
函数 的图象关于( )
的图象关于( )
| A.y轴对称 | B.直线 对称 对称 |
| C.点(1,0)对称 | D.原点对称 |
若关于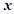 的方程
的方程 有四个不同的实数解,则实数
有四个不同的实数解,则实数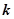 的取值范围为( )
的取值范围为( )
| A.(0,1) | B.(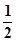 ,1) ,1) | C.(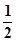 ,+∞) ,+∞) | D.(1,+∞) |
若偶函数 在
在 上是增函数,则下列关系式中成立的是( )
上是增函数,则下列关系式中成立的是( )
A. | B. |
C. | D. |
函数 ,则下列坐标表示的点一定在函数f(x)图象上的是( )
,则下列坐标表示的点一定在函数f(x)图象上的是( )
A. | B. |
C. | D. |
 ,则函数y=f(x)的大致图像为 ( )
,则函数y=f(x)的大致图像为 ( )
 ,若x=-1为函数
,若x=-1为函数 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为 的图象是( )
的图象是( )
 在
在 时是增函数,
时是增函数, 也是增函数,所以
也是增函数,所以 与
与 轴没有交点,则
轴没有交点,则 且
且 ;(3)
;(3)  的递增区间为
的递增区间为 ;(4)
;(4)  和
和 表示相等函数。
表示相等函数。


