函数f(x)＝ln x的图象与函数g(x)＝x²－4x＋4的图象的交点个数为(  )

设函数f(x)(x∈R)满足f(－x)＝f(x)，f(x)＝f(2－x)，且当x∈[0,1]时，f(x)＝x³.又函数g(x)＝|xcos(πx)|，则函数h(x)＝g(x)－f(x)在上的零点个数为(  )

函数f(x)＝ln(x²＋1)的图象大致是(  )

如图，设点A是单位圆上的一定点，动点P从A出发在圆上按逆时针方向旋转一周，点P所转过的弧AP的长为l，弦AP的长度为d，则函数d＝f(l)的图象大致是(  )

下列函数中，既是偶函数又在区间(0，＋∞)上单调递减的是(  )

A．y＝	B．y＝e－x
C．y＝－x2＋1	D．y＝lg|x|

若对于定义在R上的函数f(x)，其图象是连续不断的，且存在常数λ(λ∈R)使得f(x＋λ)＋λf(x)＝0对任意实数都成立，则称f(x)是一个“λ伴随函数”．下列关于“λ伴随函数”的结论：①f(x)＝0不是常数函数中唯一一个“λ伴随函数”；②f(x)＝x不是“λ伴随函数”；③f(x)＝x²是“λ伴随函数”；④“伴随函数”至少有一个零点．其中正确的结论个数是(  )

如图甲是某条公共汽车线路收支差额与乘客量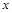的图象（收支差额=车票收入—支出费用），由于目前本条线路亏损，公司有关人员提出了两条建议：建议（Ⅰ）是不改变车票价格，减少支出费用；建议（Ⅱ）是不改变支出费用，提高车票价格.下面给出四个图象：在这些图象中(    )

设abc>0,二次函数f(x)=ax²+bx+c的图象可能是(　　)

已知函数f(x)是定义在R上的奇函数,且当x∈(-∞,0]时,f(x)=e^-x-ex²+a,则函数f(x)在x=1处的切线方程为(　　)

定义在R上的函数的图象关于点成中心对称，且对任意的实数x都有f(x)＝－f，f(－1)＝1，f(0)＝－2，则f(1)＋f(2)＋…＋f(2013)＝(　　)