设函数f(x)=x|x|+bx+c,给出下列四个命题:
①c=0时,y=f(x)是奇函数;
②b=0,c>0时,方程f(x)=0只有一个实数根;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0最多有两个实根.
其中正确的命题是( )
| A.①② | B.②④ | C.①②③ | D.①②④ |
已知函数 在
在 上的最大值为
上的最大值为 ,则函数
,则函数
的零点的个数为( )
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
函数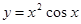 部分图象可以为( )
部分图象可以为( )
A.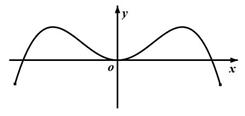 |
B.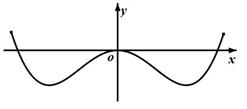 |
C.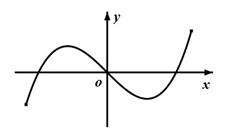 |
D.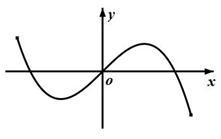 |
下列函数中,既是奇函数又在区间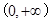 上单调递增的函数为( )
上单调递增的函数为( )
A.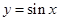 | B.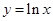 | C.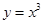 | D. |
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
已知点 是直线
是直线 上的任意一点,则
上的任意一点,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
给出以下命题:
①对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:“夹在两个平行平面间的平行线段相等”.
② =2;
=2;
③已知函数 的图象与直线
的图象与直线 有相异三个公共点,则
有相异三个公共点,则 的取值范围是(-2,2)
的取值范围是(-2,2)
其中正确命题是( )
| A.①②③ | B.①② | C.①③ | D.②③ |
观察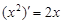 ,
,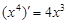 ,
,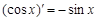 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在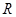 上的函数
上的函数 满足
满足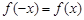 ,记
,记 为
为 的导函数,则
的导函数,则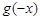 =( )
=( )
A. | B.- | C. | D.- |
 的图象大致是( )
的图象大致是( )

 ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( )