若函数y=ax与y=-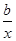 在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上( )
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上( )
| A.单调递增 | B.单调递减 |
| C.先增后减 | D.先减后增 |
若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,则f(x-1)<0的解集是( )
| A.(-1,0) | B.(-∞,0)∪(1,2) |
| C.(1,2) | D.(0,2) |
若函数f(x)、g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=ex,则有( )
| A.f(2)<f(3)<g(0) | B.g(0)<f(3)<f(2) |
| C.f(2)<g(0)<f(3) | D.g(0)<f(2)<f(3) |
若f(x)为奇函数,且在(-∞,0)内是增函数,又f(-2)=0,则xf(x)<0的解集为( )
| A.(-2,0)∪(0,2) | B.(-∞,-2)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-2,0)∪(2,+∞) |
定义在R上的偶函数f(x)在[0,+∞)上是增函数,且f( )=0,则不等式f(
)=0,则不等式f( x)>0的解集是( )
x)>0的解集是( )
A.(0,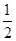 ) ) | B.(2,+∞) |
C.(0,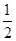 )∪(2,+∞) )∪(2,+∞) | D.(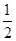 ,1)∪(2,+∞) ,1)∪(2,+∞) |
已知函数f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+m(m为常数),则f(-1)的值为( )
| A.-3 | B.-1 | C.1 | D.3 |
下列函数中,既是奇函数又是减函数的是( )
A.y=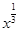 | B.y=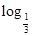 |x| |x| |
C.y=x+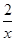 | D.y=2-x-2x |
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)( ).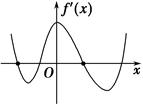
| A.无极大值点,有四个极小值点 |
| B.有三个极大值点,两个极小值点 |
| C.有两个极大值点,两个极小值点 |
| D.有四个极大值点,无极小值点 |
已知f(x+1)=f(x-1),f(x)=f(-x+2),方程f(x)=0在[0,1]内有且只有一个根x=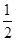 ,则f(x)=0在区间[0,2014]内根的个数为( )
,则f(x)=0在区间[0,2014]内根的个数为( )
| A.1006 | B.1007 | C.2013 | D.2014 |
f(x)的定义域为R,且f(x)=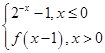 ,若方程f(x)=x+a有两个不同实根,则a的取值范围为( )
,若方程f(x)=x+a有两个不同实根,则a的取值范围为( )
| A.(-∞,1) | B.(-∞,1] |
| C.(0,1) | D.(-∞,+∞) |