题目内容
正方体ABCD-A1B1C1D1的棱长为1,在正方体内随机取点M,求使四棱锥M-ABCD的体积小于![]() 的概率.
的概率.
答案:
解析:
解析:
|
解:设点M到平面ABCD的距离为h,则V四棱锥M-ABCD= 点评:为了求出所有符合条件的点,需要找到一个符合条件的临界点,这里体现了点、线、面的相互转化. |

练习册系列答案
相关题目
 (2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1.
(2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1. (B)
(B)
 (C)
(C)
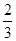 (D)
(D)

