题目内容
正方体ABCD-A1B1C1D1中,判断下列命题是否正确,并请说明理由.

(1)直线AC1在平面CC1B1B内;
(2)设正方形ABCD与A1B1C1D1的中心分别为O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1;
(3)由点A、O、C可以确定一个平面;
(4)由A、C1、B1确定的平面是ADC1B1;
(5)若直线l是平面AC内的直线,直线m是平面D1C上的直线,若l与m相交,则交点一定在直线CD上;
(6)由A、C1、B1确定的平面与由A、C1、D确定的平面是同一平面.
答案:
解析:
解析:
|
解:(1)错误.若AC1 (2)正确.O、O1是两平面的两个公共点. (3)错误.因为A、O、C共线. (4)正确.A、C1、B1不共线,∴确定平面α.又AB1C1D为平行四边形,AC1、B1D相交于O3点,而O3∈α,B1∈α,∴B1O3 (5)正确.若l与m相交,则交点是两平面的公共点,而直线CD为两平面的交线,所以交点一定在直线CD上. (6)正确.同(4). |

练习册系列答案
相关题目
 (2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1.
(2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1. (B)
(B)
 (C)
(C)
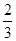 (D)
(D)

