题目内容
已知，数列{an}有a1＝a，a2＝p(常数p＞0)，对任意的正整数n，Sn＝a1＋a2＋…＋an，并有Sn满足
．
(1)求a的值；
(2)试确定数列{an}是不是等差数列，若是，求出其通项公式．若不是，说明理由；
(3)对于数列{bn}，假如存在一个常数b使得对任意的正整数n都有bn＜b且
，则称b为数列{bn}的“上渐进值”，令
，求数列{p1＋p2＋…＋pn－2n}的“上渐进值”．
答案：
解析：
解析：
|
解：(1)由已知，得 (2)由 ∴ 而n是正整数，则对任意n∈N都有 ∴数列{an}是等差数列，其通项公式是 (3)∵ ∴ 并且有 ∴数列 |
4分
，∴
，即
，于是有
，并且有
，
即
，
，
10分
；由n是正整数可得
，
，
的“上渐进值”等于3 18分
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
．
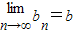，则称b为数列{bn}的“上渐进值”，令
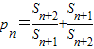，求数列{p1+p2+…+pn-2n}的“上渐进值”．
．
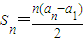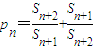，是否存在正整数M，使不等式p1+p2+…+pn-2n≤M恒成立，若存在，求出M的最小值，若不存在，说明理由．
．
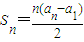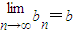，则称b为数列{bn}的“上渐进值”，令
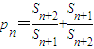，求数列{p1+p2+…+pn-2n}的“上渐进值”．