Question

已知函数f（x）=2cos2wx+2

3

coswxsinwx，（其中0＜w＜1），若直线x=

π

3

是函数f（x）图象的一条对称轴．
（1）试求w的值；
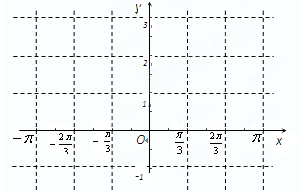
（2）先列表再作出函数f（x）在区间[-π，π]上的图象．

Answer 1

分析：（1）根据两角和差的正弦公式、二倍角公式化简函数f（x）的解析式为 1+2sin（2wx+

π

6

），再由直线x=

π

3

是函数f（x）图象的一条对称轴可得 sin（2w•

π

3

+

π

6

）=±1，由此求得w的值．
（2）用五点法作出函数在区间[-π，π]上的图象．

解答：解：（1）函数f（x）=2cos2wx+2

3

coswxsinwx=1+cos2wx+

3

sin2wx=1+2sin（2wx+

π

6

），（其中0＜w＜1），
由直线x=

π

3

是函数f（x）图象的一条对称轴可得 sin（2w•

π

3

+

π

6

）=±1，故 2w•

π

3

+

π

6

=kπ+

π

2

，k∈z．
∴w=

3k

2

+

1

2

，k∈z．∴w=

1

2

．
（2）由（1）可得函数f（x）=1+2sin（x+

π

6

），列表：

x+ π 6	- 5π 6	- π 2	0	π 2	π	7π 6
x	-π	- 2π 3	- π 6	π 3	5π 6	π
y	0	-1	1	3	1	0

作图如下：

点评：本题主要考查两角和差的正弦公式、二倍角公式的应用，用五点法作出函数y=Asin（ωx+∅）在一个周期上的简图，属于中档题．