题目内容
在△ABC中,a,b,c分别为三个内角A、B、C所对的边,设向量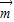 =(b+c,c-a),
=(b+c,c-a),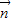 =(b,c+a),若向量
=(b,c+a),若向量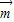 ⊥
⊥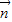 ,则角A的大小为( )
,则角A的大小为( )A.
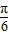
B.
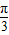
C.
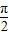
D.
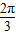
【答案】分析:根据两个向量 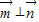 ,得到两个向量的数量积等于0,可以求得三角形三边的关系,在利用三边关系求得角A.
,得到两个向量的数量积等于0,可以求得三角形三边的关系,在利用三边关系求得角A.
解答:解:∵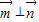 ,
,
∴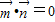 ,
,
∴(b+c)b+(c-a)(c+a)=0,
∴b2+c2-a2=-bc,
∴cosA=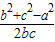 =-
=- ,
,
又因为是在三角形中,
∴A=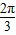
故选D.
点评:本题是一个解三角形的问题,兼有向量与余弦定理的运算,由于向量兼有代数和几何两个方面的重要特征,解决这类问题时,首先要重视对向量表达式的理解;其次要善于运用向量的坐标运算,解决问题.
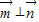 ,得到两个向量的数量积等于0,可以求得三角形三边的关系,在利用三边关系求得角A.
,得到两个向量的数量积等于0,可以求得三角形三边的关系,在利用三边关系求得角A.解答:解:∵
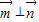 ,
,∴
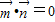 ,
,∴(b+c)b+(c-a)(c+a)=0,
∴b2+c2-a2=-bc,
∴cosA=
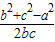 =-
=- ,
,又因为是在三角形中,
∴A=
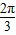
故选D.
点评:本题是一个解三角形的问题,兼有向量与余弦定理的运算,由于向量兼有代数和几何两个方面的重要特征,解决这类问题时,首先要重视对向量表达式的理解;其次要善于运用向量的坐标运算,解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|