题目内容
已知数列![]() 为等差数列,
为等差数列,![]() ,且其前
,且其前![]() 项和为
项和为![]() ,又正项数列
,又正项数列![]() 满足
满足![]()
⑴求数列![]() 的通项公式;
的通项公式;
⑵比较![]() 的大小;
的大小;
⑶求数列![]() 的最大项;
的最大项;
⑷令![]() ,数列
,数列![]() 是等比数列吗?说明理由。
是等比数列吗?说明理由。
解:⑴设![]() 的公差为
的公差为![]() ,则
,则![]()
且![]() ,得
,得![]() ,从而
,从而![]()
故![]()
⑵![]()
![]()
![]()
![]()
⑶由(2)猜想![]() 递减,即猜想当
递减,即猜想当![]() ≥
≥![]() 时,
时,![]()
考察函数![]() ,当
,当![]() 时
时![]()
![]()
故![]() 在
在![]() 上是减函数,而
上是减函数,而![]() ≥
≥![]()
所以![]() ,即
,即![]()
于是猜想正确,因此,数列![]() 的最大项是
的最大项是![]()
⑷![]() 不是等比数列
不是等比数列
由![]() 知
知
![]()
![]()
![]()
故![]() 不是等比数列。
不是等比数列。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 为等差数列,且
为等差数列,且 ,
, .
. 的通项公式;
的通项公式;  ,
, 恒成立的实数m是否存在最小值?如果存在,求出m的最小值;如果不存在,说明理由.
恒成立的实数m是否存在最小值?如果存在,求出m的最小值;如果不存在,说明理由. 为等差数列,若
为等差数列,若 且它们的前
且它们的前 项和
项和 有最大值,则使得
有最大值,则使得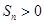 的
的 为等差数列,若
为等差数列,若 ,且它们的前
,且它们的前 项和
项和 有最大值,则使得
有最大值,则使得 的
的 为等差数列,
为等差数列,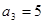 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且有
,且有
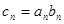 ,
, 的前
的前 ,求
,求