题目内容
等比数列{an}中,a1=512,公比q=- ,用Mn表示它的前n项之积,即Mn=a1•a2•a3…an,则数列{Mn}中的最大项是
,用Mn表示它的前n项之积,即Mn=a1•a2•a3…an,则数列{Mn}中的最大项是
- A.M11
- B.M10
- C.M9
- D.M8
C
分析:确定数列的通项,求出Mn,即可求得数列{Mn}中的最大项.
解答:由题设an=512•(- )n-1,
)n-1,
∴Mn=a1•a2•a3…an=[512×(- )0]×[512×(-
)0]×[512×(- )1]×[512×(-
)1]×[512×(- )2]×…×[512×(-
)2]×…×[512×(- )n-1]=512n×(-
)n-1]=512n×(- )1+2+3+…+(n-1)
)1+2+3+…+(n-1)
=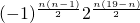
∵ =
= ,
,
∴n=9或10时,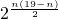 取最大值,且n=9时,
取最大值,且n=9时,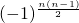 =1;n=10时,
=1;n=10时,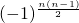 =-1,
=-1,
∴M9最大.
故选C.
点评:本题考查等比数列的通项公式,考查学生的计算能力,属于基础题.此题若直接用列举法可很简明求解:a1=512,a2=-256,a3=128,a4=-64,a5=32,a6=-16,a7=8,a8=-4,a9=2,a10=-1,当n≥11时,|an|<1,又M9>0,M10<0,故M9最大.
分析:确定数列的通项,求出Mn,即可求得数列{Mn}中的最大项.
解答:由题设an=512•(-
 )n-1,
)n-1,∴Mn=a1•a2•a3…an=[512×(-
 )0]×[512×(-
)0]×[512×(- )1]×[512×(-
)1]×[512×(- )2]×…×[512×(-
)2]×…×[512×(- )n-1]=512n×(-
)n-1]=512n×(- )1+2+3+…+(n-1)
)1+2+3+…+(n-1)=
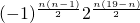
∵
 =
= ,
,∴n=9或10时,
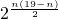 取最大值,且n=9时,
取最大值,且n=9时,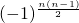 =1;n=10时,
=1;n=10时,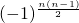 =-1,
=-1,∴M9最大.
故选C.
点评:本题考查等比数列的通项公式,考查学生的计算能力,属于基础题.此题若直接用列举法可很简明求解:a1=512,a2=-256,a3=128,a4=-64,a5=32,a6=-16,a7=8,a8=-4,a9=2,a10=-1,当n≥11时,|an|<1,又M9>0,M10<0,故M9最大.

练习册系列答案
相关题目