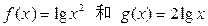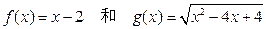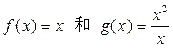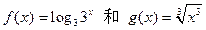题目内容
(本小题满 分12分)
分12分)
对于函数 若存在
若存在 ,使
,使 成立,则称
成立,则称 为
为 的不动点。已知函数
的不动点。已知函数
(1)当 时,求
时,求 的不动点;
的不动点;
(2)若对于任意实数 ,函数
,函数 恒有两个相异不动点,求
恒有两个相异不动点,求 的取值范围
的取值范围 。
。
 分12分)
分12分)对于函数
 若存在
若存在 ,使
,使 成立,则称
成立,则称 为
为 的不动点。已知函数
的不动点。已知函数
(1)当
 时,求
时,求 的不动点;
的不动点;(2)若对于任意实数
 ,函数
,函数 恒有两个相异不动点,求
恒有两个相异不动点,求 的取值范围
的取值范围 。
。(1)
解得 和3是函数的两个不动点
和3是函数的两个不动点
(2)

解得
 和3是函数的两个不动点
和3是函数的两个不动点(2)

解:(1) ,因为
,因为 为不动点,所以
为不动点,所以
解得 和3是函数的两个不动点, …………(4分)
和3是函数的两个不动点, …………(4分)
(2)因为函数 恒有两个相异的不动点,
恒有两个相异的不动点,
所以方程
也 就是
就是 对任何实数
对任何实数 恒有两个不相等的实数根,
恒有两个不相等的实数根,
即 对任意的
对任意的 恒成立, …………(8分)
恒成立, …………(8分)
这个不等式可化为
所以 ,解得
,解得 …………(12分)
…………(12分)
 ,因为
,因为 为不动点,所以
为不动点,所以
解得
 和3是函数的两个不动点, …………(4分)
和3是函数的两个不动点, …………(4分)(2)因为函数
 恒有两个相异的不动点,
恒有两个相异的不动点,所以方程

也
 就是
就是 对任何实数
对任何实数 恒有两个不相等的实数根,
恒有两个不相等的实数根,即
 对任意的
对任意的 恒成立, …………(8分)
恒成立, …………(8分)这个不等式可化为

所以
 ,解得
,解得 …………(12分)
…………(12分)
练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 函数f(x)=
函数f(x)=
 的值。
的值。 上是增函数。
上是增函数。
 =
= ( )
( )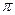 的奇函数的为
的奇函数的为
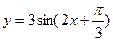
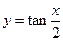
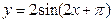
 0在[0,2]上有根,则实数m的取值范围是________.
0在[0,2]上有根,则实数m的取值范围是________.  的解是
的解是
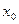 是方程式
是方程式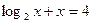 的解,则
的解,则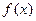 与
与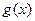 表示同一函数的一组是 ( )
表示同一函数的一组是 ( )