题目内容
(不等式选讲选做题) 若不等式|x+1|+|x-2|<a无实数解,则a的取值范围是________.
(-∞,3]
分析:由绝对值的意义可得|x+1|+|x-2|的最小值等于3,再由不等式|x+1|+|x-2|<a无实数解,则a小于或等于3,从而求得a的取值范围.
解答:由于|x+1|+|x-2|表示数轴上的x对应点到-1和2对应点的距离之和,它的最小值等于3,不等式|x+1|+|x-2|<a无实数解,
故a≤3,
故答案为(-∞,3].
点评:本题主要考查绝对值的意义,绝对值不等式的解法,属于中档题.
分析:由绝对值的意义可得|x+1|+|x-2|的最小值等于3,再由不等式|x+1|+|x-2|<a无实数解,则a小于或等于3,从而求得a的取值范围.
解答:由于|x+1|+|x-2|表示数轴上的x对应点到-1和2对应点的距离之和,它的最小值等于3,不等式|x+1|+|x-2|<a无实数解,
故a≤3,
故答案为(-∞,3].
点评:本题主要考查绝对值的意义,绝对值不等式的解法,属于中档题.

练习册系列答案
相关题目
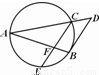
 ,则线段CD的长为 .
,则线段CD的长为 .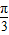 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .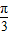 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .