题目内容

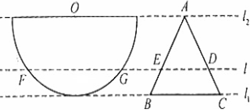
如图：l1，l2，l3，l4是同一平面内的四条平行直线，且每相邻的两条平行直线间的距离都是h，正方形ABCD的四个顶点分别在这四条直线上，且正方形的边长为5，则h=（　　）
A．
5
4
B．
5
2
C．
5
D．
10
精英家教网

精英家教网
过A点作AH⊥BE于H点．
∵S△ABE=S△FBE=S△EDF=S△CDF，
又∵正方形ABCD的面积是25，
∴S△ABE=
25
4
，且AB=AD=5，（7分）
又∵l1∥l2∥l3∥l4，
∴E、F分别是AD与BC的中点，
∴AE=
1
2
AD=
5
2
，
∴在Rt△ABE中，
BE=
AB2+AE2
=
5
5
2
，（10分）
又∵AB?AE=BE?AH，
∴AH=
AB?AE
BE
=
5×
5
2
5
5
2
=
5
．（12分）
故选C．
练习册系列答案
相关题目
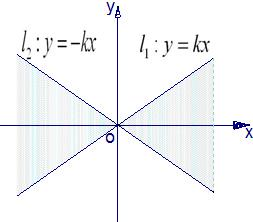精英家教网如图，直线l1：y=kx（k＞0）与直线l2：y=-kx之间的阴影区域（不含边界）记为W，其左半部分记为W1，右半部分记为W2．
（Ⅰ）分别用不等式组表示W1和W2．
（Ⅱ）若区域W中的动点P（x，y）到l1，l2的距离之积等于d2，求点P的轨迹C的方程；
（Ⅲ）设不过原点O的直线l与（Ⅱ）中的曲线C相交于M1，M2两点，且与l1，l2分别交于M3，M4两点．求证△OM1M2的重心与△OM3M4的重心重合．
已知二次函数f（x）=3x2-3x直线l1：x=2和l2：y=3tx，其中t为常数且0＜＜1．直线l2与函数f（x）的图象以及直线l1、l2与函数f（x）的图象围成的封闭图形如图中阴影所示，设这两个阴影区域的面积之和为S（t）．
（1）求函数S（t）的解析式；
（2）若函数L（t）=S（t）+6t-2，判断L（t）是否存在极值，若存在，求出极值，若不存在，说明理由；
（3）定义函数h（x）=S（x），x∈R若过点A（1，m）（m≠4）可作曲线y=h（x）（x∈R）的三条切线，求实数m的取值范围．

如图，l1∥l2，l∩l1＝A，l∩l2＝B，求证：直线l、l1、l2共面．

如果三条平行线都与一条直线相交，那么这四条直线共面．

分析：可先由已知条件分别确定平面，然后再证它们是重合的．此题可用归一法证明．

已知：如图，l1∥l2∥l3，l∩l1＝A，l∩l2＝B，l∩l3＝C．

求证：l1、l2、l3、l四条直线共面．

如图，半径为1的半圆O与等边三角形ABC夹在两平行线，l1，l2之间l∥l1，l与半圆相交于F，G两点，与三角形ABC两边相交于E，D两点，设弧的长为x(0＜x＜π)，y＝EB＋BC＋CD，若l从l1平行移动到l2，则函数y＝f(x)的图像大致是

[　　]

A．

B．

C．

D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网