题目内容
【题目】已知点![]() ,直线
,直线![]() ,且点
,且点![]() 不在直线
不在直线![]() 上.
上.
(1)若点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,求
,求![]() 点坐标;
点坐标;
(2)求证:点![]() 到直线
到直线![]() 的距离
的距离![]() ;
;
(3)当点![]() 在函数
在函数![]() 图像上时,(2)中的公式变为
图像上时,(2)中的公式变为![]() ,
,
请参考该公式,求![]()
![]() 的最小值.
的最小值.
【答案】(1)![]() ; (2)见解析; (3)
; (2)见解析; (3)![]() .
.
【解析】
(1)把握住点关于直线的对称点的关键条件是垂直与平分,列出方程组求得结果;
(2)可以利用过点作直线的垂线,求两直线的交点即垂足,再用两点间距离公式求得结果,也可以用直角三角形斜边上的高等于两直角边的乘积除以斜边长,求得结果;
(3)设出变量,利用式子,将问题转化为曲线上的点到直线的距离的最小值问题,结合图形,求得结果.
(1)因为点P,Q关于直线![]() 对称,
对称,
所以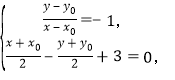
解得![]() 所以
所以![]() .
.
(2)证法一:设![]() ,根据定义,点P到直线
,根据定义,点P到直线![]() 的距离是点
的距离是点
P到直线![]() 的垂线段的长,如右图,设点P到直线
的垂线段的长,如右图,设点P到直线![]() 的垂线为
的垂线为![]() ,
,
垂足为Q,由![]() 可知
可知![]() 的斜率为
的斜率为![]() ,
,
所以![]() 的方程:
的方程:![]() .
.
与![]() 联立方程组解得交点
联立方程组解得交点![]() ,
,
所以![]()
![]()
![]()
所以![]() .
.
可证明,当![]() 时仍成立.
时仍成立.
综上![]() .
.
证法二:设![]() ,这时
,这时![]() 与
与![]() 轴、
轴、![]() 轴都相交,
轴都相交,
过点P作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ;过点P作
;过点P作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,
,
由![]() 得
得![]() ,
,
所以,![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
![]() =
=![]() ×
×![]() .
.
由三角形面积公式可知:![]() ·
·![]() =
=![]() ·
·![]() ,
,
所以![]() .
.
可证明,当![]() 或
或![]() 时仍成立.
时仍成立.
综上![]() .
.
(3)令![]() ,
,
![]() ,
,
则![]() 表示函数
表示函数![]() 图象上的点到直线
图象上的点到直线![]() 的距离,
的距离,
![]() 表示函数
表示函数![]() 图象上的点到直线
图象上的点到直线![]() 的距离,
的距离,
所以最小值为![]() .
.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目

