题目内容
已知二次函数f(x)满足条件f(0)=1,且有f(x+1)-f(x)=2x.在区间[-1,2]上,y=f(x)的图象恒在y=2x+m的图象下方,则实数m的取值范围为________.
m>5
分析:设f(x)=ax2+bx+c,根据条件求出系数a、b和c的值,再由题意转化为x2-x+1<2x+m在[-1,2]恒成立,再分离出m,进一步转化求y=x2-3x+1在[-1,2]上的最大.
解答:设二次函数f(x)=ax2+bx+c (a≠0),
∵f(0)=1,∴c=1,即f(x)=ax2+bx+1,
∵f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
即2ax+a+b=2x,∴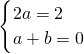 ,解得
,解得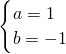 ,
,
∴f(x)=x2-x+1,
∵在区间[-1,2]上,y=f(x)的图象恒在y=2x+m的图象下方,
∴x2-x+1<2x+m,即m>x2-3x+1,x∈[-1,2],
∵y=x2-3x+1的对称轴x= ,
,
∴当x=-1时,此函数有最大值为5,
∴m>5.
故答案为:m>5.
点评:本题考查了求函数解析式方法:待定系数法,以及恒成立问题,考查了转化思想和分析、解决问题的能力.
分析:设f(x)=ax2+bx+c,根据条件求出系数a、b和c的值,再由题意转化为x2-x+1<2x+m在[-1,2]恒成立,再分离出m,进一步转化求y=x2-3x+1在[-1,2]上的最大.
解答:设二次函数f(x)=ax2+bx+c (a≠0),
∵f(0)=1,∴c=1,即f(x)=ax2+bx+1,
∵f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
即2ax+a+b=2x,∴
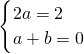 ,解得
,解得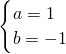 ,
,∴f(x)=x2-x+1,
∵在区间[-1,2]上,y=f(x)的图象恒在y=2x+m的图象下方,
∴x2-x+1<2x+m,即m>x2-3x+1,x∈[-1,2],
∵y=x2-3x+1的对称轴x=
 ,
,∴当x=-1时,此函数有最大值为5,
∴m>5.
故答案为:m>5.
点评:本题考查了求函数解析式方法:待定系数法,以及恒成立问题,考查了转化思想和分析、解决问题的能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目