题目内容
如图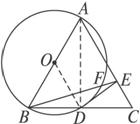
图
证明:连结OD、AD,∵AB是⊙O的直径,
∴∠ADB=90°.∴AD=BC.
∵AB=AC,∴BD=DC.
∵BO=OA,∴OD∥AC.
∵DE⊥AC,∴DE⊥OD.
∴DE是⊙O切线,∴DE2=EF·EB.①
在Rt△ACD中,DE⊥AC,
∴DE2=AE·EC.②
∴由①②得AE·EC=BE·EF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图
图
证明:连结OD、AD,∵AB是⊙O的直径,
∴∠ADB=90°.∴AD=BC.
∵AB=AC,∴BD=DC.
∵BO=OA,∴OD∥AC.
∵DE⊥AC,∴DE⊥OD.
∴DE是⊙O切线,∴DE2=EF·EB.①
在Rt△ACD中,DE⊥AC,
∴DE2=AE·EC.②
∴由①②得AE·EC=BE·EF.

 阅读快车系列答案
阅读快车系列答案