题目内容
已知二次函数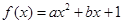 及函数
及函数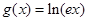 ,函数
,函数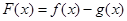 在
在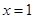 处取得极值.
处取得极值.
(Ⅰ)求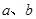 所满足的关系式;
所满足的关系式;
(Ⅱ)是否存在实数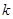 ,使得对(Ⅰ)中任意的实数
,使得对(Ⅰ)中任意的实数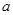 ,直线
,直线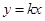 与函数
与函数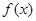 在
在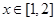 上的图像恒有公共点?若存在,求出
上的图像恒有公共点?若存在,求出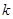 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【答案】
(Ⅰ)由已知得 ,
, ,
,
依题意得: ,即
,即 ,
……………4分
,
……………4分
代入得
要使 在
在 处有极值,则须
处有极值,则须 ,即
,即 ,
,
所以所求 满足的关系式为
满足的关系式为 . ……………5分
. ……………5分
(Ⅱ)由题意得方程 在
在 时总有解,所以
时总有解,所以
 在
在 时总有解, ……………6分
时总有解, ……………6分
设 ,则
,则 ,
……………7分
,
……………7分
①当 且
且 ,
, 时,
时, ,
, 在
在 时单调递减,
时单调递减, ,
, ,
, ;
…8分
;
…8分
②当 时,令
时,令 得:
得: ,
, 时,
时, ,
, 单调递减,
单调递减, 时,
时, ,
, 单调递增,
单调递增,
 ,
, ,
,
若 ,则
,则 ,
, ,
,
若 ,则
,则 ,
, ;
………9分
;
………9分
③当 时,
时, ,
, 在
在 时单调递增,
时单调递增,
 ,
, ,
, ; ……………10分
; ……………10分
设集合 ,
, ,
,
 ,
, ,
,
所以要使直线 与函数
与函数 在
在 上的图像恒有公共点,则实数
上的图像恒有公共点,则实数 的取值范围为:
的取值范围为: ,所以存在实数
,所以存在实数 满足题意,其取值范围为
满足题意,其取值范围为 .
.
【解析】略

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上. ,及函数
,及函数 。
。 的不等式
的不等式 的解集为
的解集为 ,其中
,其中 为正常数。
为正常数。 的值;
的值; R
R 如何取值时,函数
如何取值时,函数

 存在极值点,并求出极值点;
存在极值点,并求出极值点; ,且
,且 ,求证:
,求证:
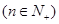 。
。