题目内容
已知函数f(x)=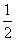 x2+lnx,
x2+lnx,
(Ⅰ)求函数f(x)在[1,e]上的最大值、最小值;
(Ⅱ)求证:在区间[1,+∞)上,函数f(x)的图象在函数g(x)=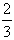 x3图象的下方;
x3图象的下方;
(Ⅲ)求证:[f′(x)]n-f′(xn)≥2n-2(n∈N*)。
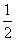 x2+lnx,
x2+lnx,(Ⅰ)求函数f(x)在[1,e]上的最大值、最小值;
(Ⅱ)求证:在区间[1,+∞)上,函数f(x)的图象在函数g(x)=
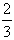 x3图象的下方;
x3图象的下方;(Ⅲ)求证:[f′(x)]n-f′(xn)≥2n-2(n∈N*)。
解:(Ⅰ)∵f′(x)=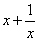 ,
,
∴当x∈[1,e]时,f′(x)>0,
∴f(x)在[1,e]上是增函数,
故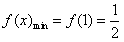 ,
,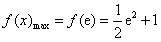 ;
;
(Ⅱ)设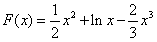 ,则
,则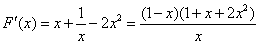 ,
,
∵x>1时,∴F′(x)<0,故F(x)在[1,+∞)上是减函数,
又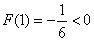 ,故在[1,+∞)上,F(x)<0,即
,故在[1,+∞)上,F(x)<0,即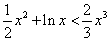 ,
,
∴函数f(x)的图象在函数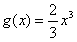 的图象的下方。
的图象的下方。
(Ⅲ)∵x>0,
∴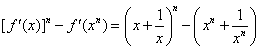 ,
,
当n=1时,不等式显然成立;
当n≥2时,有
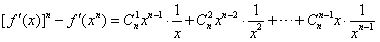
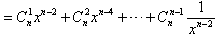
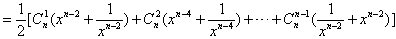
≥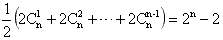 ,
,
∴[f′(x)]n-f′(xn)≥2n-2(n∈N*)。
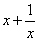 ,
,∴当x∈[1,e]时,f′(x)>0,
∴f(x)在[1,e]上是增函数,
故
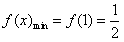 ,
,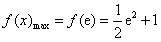 ;
;(Ⅱ)设
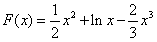 ,则
,则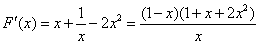 ,
,∵x>1时,∴F′(x)<0,故F(x)在[1,+∞)上是减函数,
又
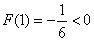 ,故在[1,+∞)上,F(x)<0,即
,故在[1,+∞)上,F(x)<0,即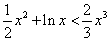 ,
, ∴函数f(x)的图象在函数
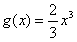 的图象的下方。
的图象的下方。(Ⅲ)∵x>0,
∴
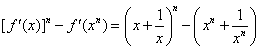 ,
,当n=1时,不等式显然成立;
当n≥2时,有
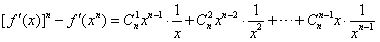
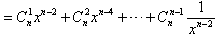
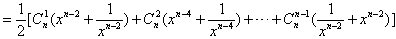
≥
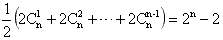 ,
,∴[f′(x)]n-f′(xn)≥2n-2(n∈N*)。

练习册系列答案
相关题目