题目内容
三棱锥P-ABC中，△ABC是底面，PA⊥PB，PA⊥PC，PB⊥PC，且这四个顶点都在半径为2的球面上，PA=2PB，则这个三棱锥的三个侧棱长的和的最大值为（ ）
| A．16 | B．
| C．
| D．32 |
∵PA，PB，PC两两垂直，
又∵三棱锥P-ABC的四个顶点均在半径为2的球面上，
∴以PA，PB，PC为棱的长方体的对角线即为球的一条直径．
∴16=PA2+PB2+PC2，又PA=2PB，∴5PB2+PC2=16，
设PB=
，PC=4sinα，
则这个三棱锥的三个侧棱长的和PA+PB+PC=3PB+PC=
cosα+4sinα=
sin（α+∅）≤
．
则这个三棱锥的三个侧棱长的和的最大值为
，
故选B．
又∵三棱锥P-ABC的四个顶点均在半径为2的球面上，
∴以PA，PB，PC为棱的长方体的对角线即为球的一条直径．
∴16=PA2+PB2+PC2，又PA=2PB，∴5PB2+PC2=16，
设PB=
| 4cosα | ||
|
则这个三棱锥的三个侧棱长的和PA+PB+PC=3PB+PC=
| 12 | ||
|
| 4 |
| 5 |
| 70 |
| 4 |
| 5 |
| 70 |
则这个三棱锥的三个侧棱长的和的最大值为
| 4 |
| 5 |
| 70 |
故选B．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
如图，在三棱锥P-ABC中，△PAB是等边三角形，∠PAC=∠PBC=90°．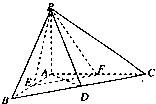
如图，在三棱锥P-ABC中，
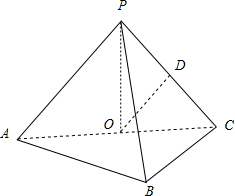如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
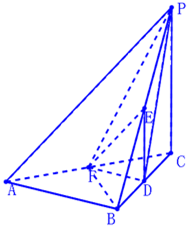如图，在三棱锥P-ABC中，PC⊥平面ABC，△ABC为正三角形，D、E、F分别是BC，PB，CA的中点．