题目内容
已知函数f(x)=lnx,g(x)= x2﹣bx(b为常数).
x2﹣bx(b为常数).
(1)函数f(x)的图象在点(1,f(1))处的切线与g(x)的图象相切,求实数b的值;
(2)设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b 的取值范围;
(3)若b>1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求b的取值范围.
 x2﹣bx(b为常数).
x2﹣bx(b为常数). (1)函数f(x)的图象在点(1,f(1))处的切线与g(x)的图象相切,求实数b的值;
(2)设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b 的取值范围;
(3)若b>1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求b的取值范围.
解:(1)f(x)=lnx得f'(x)= ,
,
函数f(x)的图象在点(1,f(1))处的切线的斜率为f'(1)=1,
切线方程为:y﹣0=x﹣1即y=x﹣1.
由已知得它与g(x)的图象相切,将y=x﹣1代入得x
﹣1= x2﹣bx,即
x2﹣bx,即 x2﹣(b+1)x+1=0,
x2﹣(b+1)x+1=0,
∴△=(b+1)2﹣2=0,解得b=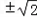 ﹣1,
﹣1,
即实数b的值为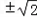 ﹣1.
﹣1.
(2)h(x)=f(x)+g(x)=lnx+ x2﹣bx,
x2﹣bx,
∴h'(x)= +x﹣b,
+x﹣b,
根据函数h(x)在定义域(0,+∞)上存在单调减区间,
∴存在x>0,使得 +x﹣b<0,即b>
+x﹣b<0,即b> +x,
+x,
由于当x>0时, +x≥2,
+x≥2,
∴b>2.
∴实数b 的取值范围(2,+∞).
(3)对于区间[1,2]上的任意实数x,f'(x)= ∈[
∈[ ,1].g'(x)=x﹣b∈[1﹣b,2﹣b],
,1].g'(x)=x﹣b∈[1﹣b,2﹣b],
要使得对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,
即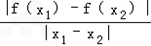 >
>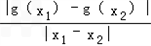 ,
,
利用导数的几何是切线的斜率,得到f'(x)最小值>g'(x)最大值,
即 >2﹣b,
>2﹣b,
∴b> .
.
则b的取值范围( ,+∞).
,+∞).
 ,
, 函数f(x)的图象在点(1,f(1))处的切线的斜率为f'(1)=1,
切线方程为:y﹣0=x﹣1即y=x﹣1.
由已知得它与g(x)的图象相切,将y=x﹣1代入得x
﹣1=
 x2﹣bx,即
x2﹣bx,即 x2﹣(b+1)x+1=0,
x2﹣(b+1)x+1=0,∴△=(b+1)2﹣2=0,解得b=
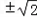 ﹣1,
﹣1,即实数b的值为
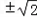 ﹣1.
﹣1.(2)h(x)=f(x)+g(x)=lnx+
 x2﹣bx,
x2﹣bx,∴h'(x)=
 +x﹣b,
+x﹣b,根据函数h(x)在定义域(0,+∞)上存在单调减区间,
∴存在x>0,使得
 +x﹣b<0,即b>
+x﹣b<0,即b> +x,
+x,由于当x>0时,
 +x≥2,
+x≥2,∴b>2.
∴实数b 的取值范围(2,+∞).
(3)对于区间[1,2]上的任意实数x,f'(x)=
 ∈[
∈[ ,1].g'(x)=x﹣b∈[1﹣b,2﹣b],
,1].g'(x)=x﹣b∈[1﹣b,2﹣b],要使得对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,
即
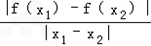 >
>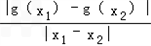 ,
,利用导数的几何是切线的斜率,得到f'(x)最小值>g'(x)最大值,
即
 >2﹣b,
>2﹣b,∴b>
 .
.则b的取值范围(
 ,+∞).
,+∞).
练习册系列答案
相关题目