题目内容
甲、乙、丙三人参加一家公司的招聘面试,面试合格者可正式签约.甲表示只要面试合格就签约,乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人合格的概率都是| 1 | 2 |
(I)至少有一人面试合格的概率;
(Ⅱ)没有人签约的概率.
分析:(I)至少有一人面试合格的对立事件是三个人面试都不合格,根据每人合格的概率都是
,且面试是否合格互不影响,做出三个人都不合格的概率,根据对立事件的概率得到结果.
(II)没有人签约包括三种情况,甲不合格,且乙和丙恰有一个不合格;甲不合格且乙和丙都不合格,这三种情况是互斥的,根据相互独立事件的概率和互斥事件的概率公式,得到结果.
| 1 |
| 2 |
(II)没有人签约包括三种情况,甲不合格,且乙和丙恰有一个不合格;甲不合格且乙和丙都不合格,这三种情况是互斥的,根据相互独立事件的概率和互斥事件的概率公式,得到结果.
解答:解:用A,B,C分别表示事件甲、乙、丙面试合格.
由题意知A,B,C相互独立,且P(A)=P(B)=P(C)=
.
(Ⅰ)至少有1人面试合格的概率是1-P(
)=1-P(
)P(
)P(
)=1-(
)3=
.
(II)没有人签约的概率为P(
B
)+P(
C)+P(
)=(
)3+(
)3+(
)3=
.
由题意知A,B,C相互独立,且P(A)=P(B)=P(C)=
| 1 |
| 2 |
(Ⅰ)至少有1人面试合格的概率是1-P(
. |
| A |
. |
| B |
. |
| C |
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 2 |
| 7 |
| 8 |
(II)没有人签约的概率为P(
. |
| A |
. |
| C |
. |
| A |
. |
| B |
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
点评:本题考查相互独立事件同时发生的概率,考查互斥事件的概率,是一个基础题,题目中对于乙和丙的叙述比较难理解,“乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.”,这里容易漏掉结果.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲、乙、丙三人参加一次考试,他们合格的概率分别为
,
,
,那么三人中恰有两人合格的概率是( )
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 ,
, ,
, ,那么三人中恰有两人合格的概率是
,那么三人中恰有两人合格的概率是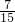
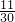

 ,
, ,
, ,那么三人中恰有两人合格的概率是( )
,那么三人中恰有两人合格的概率是( )



 ,
, ,
, ,那么三人中恰有两人合格的概率是
,那么三人中恰有两人合格的概率是


