题目内容
如图所示,四棱锥P-ABCD的底面是边长为1的正方形,PA^
CD,PA=1,PD=![]() ,E为PD上一点,PE=2ED.
,E为PD上一点,PE=2ED.

(Ⅰ)求证:PA^ 平面ABCD;
(Ⅱ)求二面角D-AC-E的余弦值;
(Ⅲ)在侧棱PC上是否存在一点F,使得BF∥平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由.
答案:
解析:

解析:
解:(Ⅰ)![]() PA=PD=1,PD=2,
PA=PD=1,PD=2,![]() PA2+AD2=PD2,即:PA^
AD 2分
PA2+AD2=PD2,即:PA^
AD 2分
又PA^
CD,AD,CD相交于点D,![]() PA^
平面ABCD 4分
PA^
平面ABCD 4分
(Ⅱ)过E作EG//PA交AD于G,从而EG^ 平面ABCD,且AG=2GD,
EG=![]() PA=
PA=![]() , 5分连接BD交AC于O,过G作GH//OD,交AC于H,
, 5分连接BD交AC于O,过G作GH//OD,交AC于H,
连接EH.![]() GH^
AC,
GH^
AC,![]() EH^
AC,
EH^
AC,![]() Ð
EHG为二面角D-AC―E的平面角. 6分
Ð
EHG为二面角D-AC―E的平面角. 6分
![]() tanÐ
EHG=
tanÐ
EHG=![]() .
.![]() 二面角D-AC―E的平面角的余弦值为
二面角D-AC―E的平面角的余弦值为![]() 8分
8分
(Ⅲ)以AB,AD,PA为x轴、y轴、z轴建立空间直角坐标系.则A(0,0,0),B(1,0,0),C(1,1,0),P(0,0,1),E(0,![]() ,
,![]() ),
),![]() =(1,1,0),
=(1,1,0),![]() =(0,
=(0,![]() ,
,![]() )---9分设平面AEC的法向量
)---9分设平面AEC的法向量![]() =(x,y,z),则
=(x,y,z),则 ,
,
即:![]() ,令y=1,则
,令y=1,则![]() =(-1,1,-2) 10分
=(-1,1,-2) 10分
假设侧棱PC上存在一点F,且![]() =
=![]()
![]() ,(0£
,(0£
![]() £
1),使得:BF//平面AEC,则
£
1),使得:BF//平面AEC,则![]() ×
×
![]() =0.又因为:
=0.又因为:![]() =
=![]() +
+![]() =(0,1,0)+(-
=(0,1,0)+(-![]() ,-
,-![]() ,
,![]() )=(-
)=(-![]() ,1-
,1-![]() ,
,![]() ),
),![]()
![]() ×
×
![]() =
=![]() +1-
+1-![]() -2
-2![]() =0,
=0,![]()
![]() =
=![]() ,所以存在PC的中点F,使得BF//平面AEC 12分
,所以存在PC的中点F,使得BF//平面AEC 12分


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.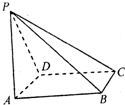 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,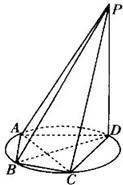 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.