题目内容
(本小题12分)命题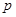 :关于
:关于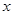 的不等式
的不等式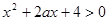 对于一切
对于一切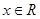 恒成立,命题
恒成立,命题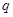 :函数
:函数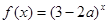 是增函数,若
是增函数,若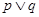 为真,
为真,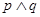 为假,求实数
为假,求实数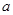 的取值范围;
的取值范围;
【答案】
{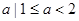 或
或 }.
}.
【解析】本题考查一元二次不等式的解法,四种命题的真假关系,指数函数的单调性与特殊点,考查计算能力,是基础题.
由题意分别求出p为真,q为真时,a的取值范围,根据p或q为真,p且q为假,就是一真一假,求出a的范围即可.
解:设
由于关于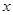 的不等式
的不等式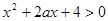 对于一切
对于一切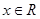 恒成立
恒成立
所以函数 的图象开口向上且与
的图象开口向上且与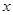 轴没有交点,
轴没有交点,
故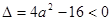 ,∴
,∴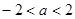 .
. -------------- 2分
-------------- 2分
函数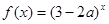 是增函数,则有
是增函数,则有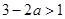 ,即
,即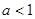 . -------4分
. -------4分
由于p或q为真,p且q为假,可知p、q一真一假. ---------------5分
①若p真q假,则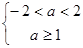 ∴
∴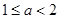 ;-------------------8分
;-------------------8分
②若p假q真,则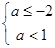
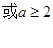 ∴
∴ ;-----------------11分
;-----------------11分
综上可知,所求实数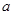 的取值范围是{
的取值范围是{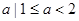 或
或 }.------12分
}.------12分

练习册系列答案
相关题目
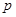 :函数
:函数 的图象与
的图象与 轴没有公共点,命题
轴没有公共点,命题 ,若命题
,若命题 为真命题,求实数
为真命题,求实数 的取值范围
的取值范围 ;
; 是增函数,
是增函数, 求实数
求实数 的取值范围
的取值范围 ;
; 是增函数,
是增函数, 求实数
求实数 的取值范围
的取值范围