题目内容
在R上可导的函数f（x）=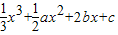
，当x∈（0，1）时取得极大值．当x∈（1，2）时取得极小值，则
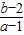的取值范围是（ ）A．
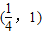
B．
C．
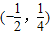
D．
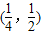
【答案】分析：由题意知f′（x）=x2+ax+2b，结合题设条件由此可以导出
的取值范围．
解答：解：∵f（x）=
，∴f′（x）=x2+ax+2b，
设x2+ax+2b=（x-x1）（x-x2），（x1＜x2）
则x1+x2=-a，x1x2=2b，
因为函数f（x）当x∈（0，1）时取得极大值，x∈（1，2）时取得极小值
∴0＜x1＜1，1＜x2＜2，
∴1＜-a＜3，0＜2b＜2，-3＜a＜-1，0＜b＜1．∴-2＜b-2＜-1，-4＜a-1＜-2，
∴
，
故选A．
点评：本题考查导数和导数的应用，解题时要注意等价命题的合理转换．
的取值范围．解答：解：∵f（x）=
，∴f′（x）=x2+ax+2b，设x2+ax+2b=（x-x1）（x-x2），（x1＜x2）
则x1+x2=-a，x1x2=2b，
因为函数f（x）当x∈（0，1）时取得极大值，x∈（1，2）时取得极小值
∴0＜x1＜1，1＜x2＜2，
∴1＜-a＜3，0＜2b＜2，-3＜a＜-1，0＜b＜1．∴-2＜b-2＜-1，-4＜a-1＜-2，
∴
，故选A．
点评：本题考查导数和导数的应用，解题时要注意等价命题的合理转换．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
7、在R上可导的函数f（x）的图象如图所示，则关于x的不等式x•f′（x）＜0的解集为（ ）
在R上可导的函数f（x）=
x3+
ax2+2bx+c，当x∈（0，1）时取得极大值．当x∈（1，2）时取得极小值，则
的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
已知在R上可导的函数f（x）的图象如图所示，则不等式f（x）•f′（x）＜0的解集为（ ）