题目内容
(本小题满分13分)
设直线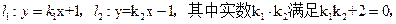
(I)证明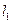 与
与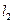 相交;
相交;
(II)证明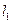 与
与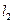 的交点在椭圆
的交点在椭圆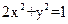 上.
上.
来源:学*科*网]
(1)(反证法)假设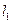 与
与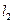 不相交,则
不相交,则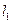 与
与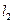 必平行,
必平行,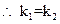 代入
代入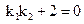 得
得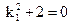 ,与
,与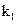 是实数相矛盾。从而
是实数相矛盾。从而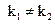 ,即
,即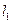 与
与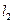 相交。
相交。
(2)(方法一)由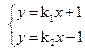 得交点p的坐标(x,y)为
得交点p的坐标(x,y)为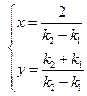 ,
,
而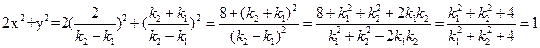
所以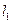 与
与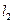 的交点p的(x,y)在椭圆
的交点p的(x,y)在椭圆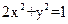 上
上
(方法二)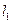 与
与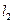 的交点p的(x,y)满足:
的交点p的(x,y)满足: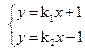 ,
,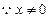 ,从而
,从而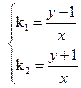 ,代入
,代入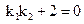 得
得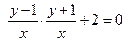 ,整理得
,整理得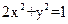
所以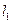 与
与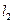 的交点p的(x,y)在椭圆
的交点p的(x,y)在椭圆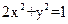 上
上
【解题指导】:两直线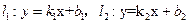 的位置关系判定方法:
的位置关系判定方法:
(1)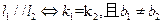
(2)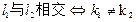
(3)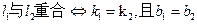
证明两数不等可采用反证法的思路。
点在线上的判断与证明只要将点的坐标代入曲线方程判断其是否成立即可,或求出交点的轨迹方程并判断与所给的曲线方程是否一致即可。本题属于中档题。[
解析

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和