题目内容
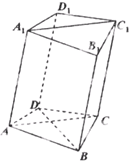 (2013•黄冈模拟)如图,在四棱柱ABCD-A1B1C1D1中,已 知平面AA1C1C丄平面ABCD,且AB=BC=CA=
(2013•黄冈模拟)如图,在四棱柱ABCD-A1B1C1D1中,已 知平面AA1C1C丄平面ABCD,且AB=BC=CA=| 3 |
(I)求证:BD丄AA1;
(II)若四边形ACC1A1是菱形,且∠A1AC=60°,求四棱柱 ABCD-A1B1C1D1 的体积.
分析:(I)利用垂直平分线的判定定理即可得到BD垂直平分AC,利用面面垂直的性质定理即可得到BD⊥平面AA1C1C,利用线面垂直的性质定理即可证明结论;
(II)过点A1作A1E丄AC于点E,即A1E为四棱柱的一条高.又由四边形AA1C1C是菱形,则得四棱柱ABCD-A1B1C1D1的高为h=
,再由四棱柱ABCD-A1B1C1D1的底面面积为
,即可得到四棱柱ABCD-A1B1C1D1的体积.
(II)过点A1作A1E丄AC于点E,即A1E为四棱柱的一条高.又由四边形AA1C1C是菱形,则得四棱柱ABCD-A1B1C1D1的高为h=
| 3 |
| 2 |
| 3 |
解答: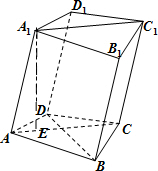 解:(Ⅰ)在四边形ABCD中,∵BA=BC,DA=DC,∴BD⊥AC.
解:(Ⅰ)在四边形ABCD中,∵BA=BC,DA=DC,∴BD⊥AC.
又∵平面AA1C1C丄平面ABCD,且平面AA1C1C∩平面ABCD=AC,BD?平面ABCD,
∴BD丄平面AA1C1C.
又∵AA1?平面AA1C1C,
∴BD丄AA1;
(Ⅱ)过点A1作A1E丄AC于点E,
∵平面AA1C1C丄平面ABCD,
∴A1E丄平面ABCD,
即A1E为四棱柱的一条高.
又∵四边形AA1C1C是菱形,且∠A1AC=60°,
∴四棱柱ABCD-A1B1C1D1的高为h=A1E=
sin60°=
又∵四棱柱ABCD-A1B1C1D1的底面面积SABCD=
|AC||BD|=
×
×(
+
)=
,
∴四棱柱ABCD-A1B1C1D1的体积为V=
×
=
.
 解:(Ⅰ)在四边形ABCD中,∵BA=BC,DA=DC,∴BD⊥AC.
解:(Ⅰ)在四边形ABCD中,∵BA=BC,DA=DC,∴BD⊥AC. 又∵平面AA1C1C丄平面ABCD,且平面AA1C1C∩平面ABCD=AC,BD?平面ABCD,
∴BD丄平面AA1C1C.
又∵AA1?平面AA1C1C,
∴BD丄AA1;
(Ⅱ)过点A1作A1E丄AC于点E,
∵平面AA1C1C丄平面ABCD,
∴A1E丄平面ABCD,
即A1E为四棱柱的一条高.
又∵四边形AA1C1C是菱形,且∠A1AC=60°,
∴四棱柱ABCD-A1B1C1D1的高为h=A1E=
| 3 |
| 3 |
| 2 |
又∵四棱柱ABCD-A1B1C1D1的底面面积SABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
∴四棱柱ABCD-A1B1C1D1的体积为V=
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
点评:熟练掌握垂直平分线的判定定理、面面垂直的性质定理、直角△OCD的边角关系、等边三角形的性质、线面平行的判定定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 (2013•黄冈模拟)如图所示程序框图的输出的所有值都在函数( )
(2013•黄冈模拟)如图所示程序框图的输出的所有值都在函数( )